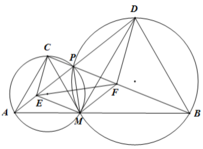
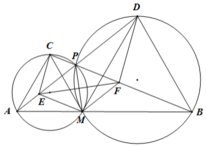
Cho ba điểm A, M, B phân biệt, thẳng hàng và M nằm giữa A, B. Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, dựng hai tam giác đều AMC và BMD. Gọi P là giao điểm của AD và BC.
b) Chứng minh C P . C B + D P . D A = A B
c) Đường thẳng nối tâm của hai đường tròn ngoại tiếp hai tứ giác AMPC và BMPD cắt PA, PB tương ứng tại E, F. Chứng minh CDFE là hình thang.

.png)

b) Vì AMPC là tứ giác nội tiếp nên
C P M = 180 o − C A M = 120 o = C M B ⇒ Δ C P M ~ Δ C M B ( g . g ) ⇒ C P C M = C M C B ⇒ C P . C B = C M 2 ⇒ C P . C B = C M .
Tương tự D P . D A = D M
Vậy C P . C B + D P . D A = C M + D M = A M + B M = A B