Tập nghiệm của phương trình là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn

Ta có: \({x^2} + x - 2 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\\x = - 2\end{array} \right.\)
\( \Rightarrow A = \{ 1; - 2\} \)
Ta có: \(2{x^2} + x - 6 = 0 \Leftrightarrow \left[ \begin{array}{l}x = \frac{3}{2}\\x = - 2\end{array} \right.\)
\( \Rightarrow B = \left\{ {\frac{3}{2}; - 2} \right\}\)
Vậy \(C = A \cap B = \{ - 2\} \).

\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\)
\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)
\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)
\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)
\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)
\(\Leftrightarrow VT\le2g\left(x\right)\)
Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)
\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)
Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)
Ta có:
\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)
\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)
Vậy tập nghiệm của pt đã cho có đúng 1 phần tử


Chọn D
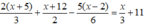
⇔ 4(x + 5) + 3(x + 12) - 5(x – 2) = 2x + 66
⇔ 4x + 20 + 3x + 36 – 5x + 10 = 2x + 66
⇔ 0x = 0 (thỏa mãn mọi giá trị của x)
Vậy phương trình đã cho có vô số nghiệm.

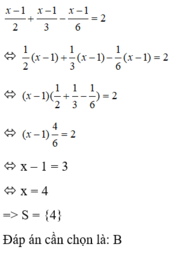
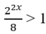
Điều kiện: 3 x 2 + 6 x + 16 ≥ 0 x 2 + 2 x ≥ 0 x 2 + 2 x + 4 ≥ 0 ⇔ x ≤ − 2 x ≥ 0
Đặt t = x 2 + 2 x ( t ≥ 0 ) ⇔ t 2 = x 2 + 2 x
Phương trình trở thành: 3 t 2 + 16 + t = 2 t 2 + 4
⇔ 3 t 2 + 16 + t 2 + 2 t 3 t 2 + 16 = 4 t 2 + 16 ⇔ 2 t 3 t 2 + 16 = 0 ⇔ t = 0
Với t = 0 ⇔ x 2 + 2 x = 0 ⇔ x = 0 x = − 2
Vậy tập nghiệm của phương trình là: S = 0 ; − 2
Đáp án cần chọn là: A