Cho anđehit cộng H2 theo phản ứng sau: CnH2n+1-2aCHO + xH2 → CnH2n+1CH2OH. Hệ số x của H2 bằng
A. a + 1
B. 2a
C. a/2
D. a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp C
Gọi số mol của C n H 2 n − 1 C H O , C n H 2 n − 1 C O O H , C n H 2 n − 1 C H 2 O H trong X lần lượt là x,y,z.
Có n B r 2 = 2 x + y + z = 8 , 8 160 = 0 , 055 m o l
x = 1 2 n A g = 1 2 . 2 , 16 108 = 0 , 01 m o l ⇒ x + y + z = 0 , 055 − 0 , 01 = 0 , 045 ⇒ M ¯ X = 2 , 8 0 , 045 = 62 , 22 ⇒ M C n H 2 n − 1 C H O < 62 , 22 < M C n H 2 n − 1 C O O H ⇔ 14 n + 28 < 62 , 22 < 14 n + 44 ⇔ 1 , 3 < n < 2 , 4 ⇒ n = 2 % m C 2 H 3 C H O = 56.0 , 01 2 , 8 .100 % = 20 %
2,8 g X phản ứng với tối đa 0,045 mol H2
m g X phản ứng với tối đa 0,3 mol H2
⇒ m = 0 , 09 0 , 045 .2 , 8 = 5 , 6 g

Sửa đề: 44,4 → 4,44
a, \(CH_3COOH+Na\rightarrow CH_3COONa+\dfrac{1}{2}H_2\)
\(C_nH_{2n+1}COOH+Na\rightarrow C_nH_{2n+1}COONa+\dfrac{1}{2}H_2\)
b, Gọi: nCH3COOH = 2x (mol) ⇒ nCnH2n+1COOH = x (mol)
\(n_{H_2}=\dfrac{0,672}{22,4}=0,03\left(mol\right)\)
Theo PT: \(n_{H_2}=\dfrac{1}{2}n_{CH_3COOH}+\dfrac{1}{2}n_{C_nH_{2n+1}COOH}=x+\dfrac{1}{2}x=0,03\)
⇒ x = 0,02 (mol)
⇒ nCH3COOH = 0,04 (mol), nCnH2n+1COOH = 0,02 (mol)
\(\Rightarrow0,04.60+0,02.\left(14n+46\right)=4,44\Rightarrow n=4\)
Vậy: B là C4H9COOH.
c, \(\left\{{}\begin{matrix}\%m_{CH_3COOH}=\dfrac{0,04.60}{4,44}.100\%\approx54,05\%\\\%m_{C_4H_9COOH}\approx45,95\%\end{matrix}\right.\)

Đáp án A.
Gọi số mol các chất lần lượt là: a, b, c
Ta có:
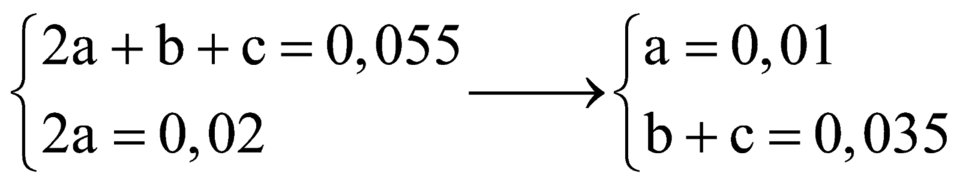
Nhận thấy, nếu gốc hidrocacbon mà lớn hơn CH2 = CH – thì khối lương hỗn hợp X sẽ vô lý.
![]()

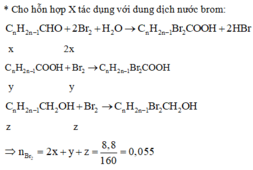
Nhận thấy phương trình (*) có 3 ẩn mà chỉ có 1 phương trình nên không thể tìm giá trị của n. Khi đó nhiều bạn sẽ cho rằng đề thiếu dữ kiện và không thể giải tiếp.
Tuy nhiên chúng ta có thể sử dụng bất đẳng thức để tìm giá trị của n như sau:

Đáp án B
Hướng dẫn giải
CnH2n+1-2aCHO + (a + 1)H2 → CnH2n+1CH2OH
Chọn A