Số nghiệm của phương trình sin2x = 3 2 trong khoảng (0; 3π) là
A.1
B.2
C.6
D.4
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 10 2017
Phương trình ⇔ 1 2 sin 2 x + 3 2 cos 2 x = 3 2 ⇔ sin 2 x + π 3 = 3 2
⇔ sin 2 x + π 3 = sin π 3 ⇔ 2 x + π 3 = π 3 + k 2 π 2 x + π 3 = π − π 3 + k 2 π ⇔ x = k π x = π 6 + k π , k ∈ ℤ .
= 0 < k π < π 2 ⇔ 0 < k < 1 2 → k ∈ ℤ không có giá trị k thỏa mãn.
= 0 < π 6 + k π < π 2 ⇔ − 1 6 < k < 1 3 → k ∈ ℤ k = 0 → x = π 6 .
Chọn đáp án A.
CM
11 tháng 3 2017
Chọn C
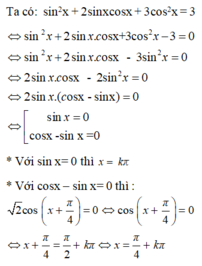
Vậy các nghiệm thuộc khoảng (0, 2π) là π 4 , π , 5 π 4
17 tháng 7 2021
Pt \(\Leftrightarrow2sin\left(2x+\dfrac{\pi}{3}\right)=\sqrt{3}\)
\(\Leftrightarrow sin\left(2x+\dfrac{\pi}{3}\right)=\dfrac{\sqrt{3}}{2}\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{6}+k\pi\\x=k\pi\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(x\in\left(0;\dfrac{\pi}{2}\right)\)\(\Rightarrow\left[{}\begin{matrix}0< \dfrac{\pi}{6}+k\pi< \dfrac{\pi}{2}\\0< k\pi< \dfrac{\pi}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)
\(\Leftrightarrow\left[{}\begin{matrix}-\dfrac{1}{6}< k< \dfrac{1}{3}\\0< k< \dfrac{1}{2}\end{matrix}\right.\)\(\left(k\in Z\right)\)\(\Leftrightarrow\left[{}\begin{matrix}k=0\\k\in\varnothing\end{matrix}\right.\)
Vậy có 1 nghiệm thỏa mãn
PT
1
CM
5 tháng 7 2019
Đáp án A
Ta có c o s x + sin 2 x = 0 ⇔ cos x + 2 sin x cos x = 0 ⇔ [ cos x = 0 sin x = - 1 2 ⇔ [ x = π 2 + k π x = - π 6 + k 2 π x = 7 π 6 + k 2 π
Mà x ∈ - π ; π ⇒ x ∈ - π 2 ; π 2 ; - π 6 ; - 5 π 6 .
PT
1
PT
1
CM
27 tháng 9 2017
Đáp án A
sin 2 x = c os2x ⇔ 2 sin ( 2 x − π 4 ) = 0 ⇔ 2 x = π 4 + k π ⇔ x = π 8 + k π 2
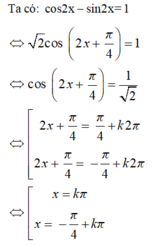
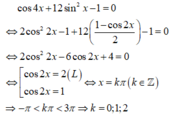
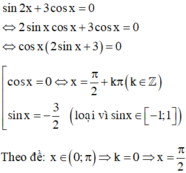
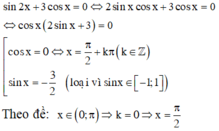
Đáp án C