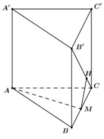
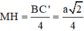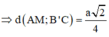Cho hình lăng trụ đứng ABC.A’B’C’ có đáy ABC là tam giác vuông, BA=BC=a, cạnh bên A A ' = a 2 , M là trung điểm của BC. Khoảng cách giữa hai đường thẳng AM và B’C bằng
A. a 2 2
B. a 3 3
C. a 5 5
D. a 7 7
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là A
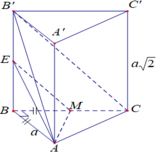
Gọi E là trung điểm của B B ' . Khi đó B ' C / / A M E ⇒ d A M ; B ' C = d B ' C ; A M E .
Mặt khác d B ; A M E = d C ; A M E . Gọi h = d B ; A M E
Vì tứ diện B A M E có B A ; B M ; B E đôi một vuông góc với nhau.
⇒ 1 h 2 = 1 B A 2 + 1 B M 2 + 1 B E 2 ⇒ 1 h 2 = 1 a 2 + 4 a 2 + 2 a 2 = 7 a 2 ⇒ h = a 7 7 ⇒ d B ' C ; A M = a 7 7 .

Đặt hệ trục Oxyz vào lăng trụ, với gốc O trùng B, tia BA trùng Ox, tia BC trùng Oy, tia BB' trùng Oz. Quy ước a là 1 đơn vị độ dài.
Ta có tọa độ các điểm: \(A\left(2;0;0\right)\) ; \(B\left(0;0;0\right)\) ; \(C\left(0;2;0\right)\); \(B'\left(0;0;2\sqrt{2}\right)\)
Do M là trung điểm BC \(\Rightarrow M\left(0;1;0\right)\)
\(\overrightarrow{u_{AM}}=\overrightarrow{AM}=\left(-2;1;0\right)\); \(\overrightarrow{u_{B'C}}=\overrightarrow{B'C}=\left(0;2;-2\sqrt{2}\right)\)
\(\overrightarrow{AC}=\left(-2;2;0\right)\) (A là điểm thuộc đường AM, C là điểm thuộc đường B'C)
\(\left[\overrightarrow{u_{AM}};\overrightarrow{u_{B'C}}\right]=\left[-2\sqrt{2};-4\sqrt{2};-4\right]\)
Áp dụng công thức k/c hai đường chéo nhau:
\(d\left(AM;B'C\right)=\dfrac{\left|\left[\overrightarrow{u_{AM}};\overrightarrow{u_{B'C}}\right].\overrightarrow{AC}\right|}{\left|\left[\overrightarrow{u_{AM}};\overrightarrow{u_{B'C}}\right]\right|}=\dfrac{2a\sqrt{7}}{7}\) (sau khi đã đổi lại 1 đơn vị độ dài bằng a)
Bạn kiểm tra lại tính toán
Em chào anh ạ! Sau bao lâu anh cũng online, anh vào giúp em câu này ạ, có lời giải trên mạng em không hiểu vì sao có rất nhiều cặp số chia hết cho 3 nhưng người ta chỉ lấy 7 cặp thôi, chưa đủ anh ạ!
https://hoc24.vn/cau-hoi/cho-tap-hop-so-a-0123456hoi-co-the-thanh-lap-bao-nhieu-so-co-4-chu-so-khac-nhau-va-chia-het-cho-3.7684280688607

Đáp án B
Phương pháp : Dụng đường vuông góc chung.
Cách giải :
Ta có: 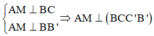
Trong (BCC’B’) kẻ ![]()
![]()
=>MH là đoạn vuông góc chung giữa AM và B’C ![]()
Dễ thấy