Tìm độ dài khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = x3 + 3x2 – 4? A. 2√5 B. 4√5 C. 6√5 D....
Đọc tiếp
Tìm độ dài khoảng cách giữa hai điểm cực trị của đồ thị hàm số y = x3 + 3x2 – 4?
A. 2√5
B. 4√5
C. 6√5
D. 8√5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 3 2017
Đáp án: D.
y' = 3 x 2 + 3x = 3x(x + 1) = 0
⇔ 
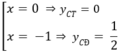
Vậy khoảng cách giữa hai điểm cực trị là:
PT
1
CM
28 tháng 3 2019
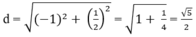
Đáp án C
D = ℝ ; y ' = 3 x 2 + 6 x ; y ' = 0 ⇔ x = 0 x = − 2
Tọa độ 2 điểm cực trị A 0 ; − 4 , B − 2 ; 0
Khoảng cách giữa hai điểm cực trị là A B = x B − x A 2 + y B − y A 2 = 20 = 2 5
CM
24 tháng 7 2019
Đáp án: D.
y' = 3 x 2 + 3x = 3x(x + 1) = 0
⇔ 
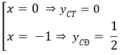
Vậy khoảng cách giữa hai điểm cực trị là:
BA
21 tháng 11 2023
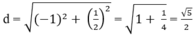
Đầu tiên, ta cần tìm điểm cực trị của hàm số f(x) = x^3 - 3x^2 + m. Điều kiện cần và đủ để x_0 là điểm cực trị của hàm số y = f(x) là f’(x_0) = 0 và f’'(x_0) ≠ 0.
Ta có f’(x) = 3x^2 - 6x và f’'(x) = 6x - 6.
Giải phương trình f’(x) = 0, ta được x_1 = 0 và x_2 = 2. Kiểm tra điều kiện thứ hai, ta thấy f’‘(0) = -6 ≠ 0 và f’'(2) = 6 ≠ 0 nên x_1 = 0 và x_2 = 2 là hai điểm cực trị của hàm số.
Vậy, A = (0, f(0)) = (0, m) và B = (2, f(2)) = (2, 4 - m).
Trọng tâm G của tam giác OAB có tọa độ (x_G, y_G) = (1/3 * (x_A + x_B + x_O), 1/3 * (y_A + y_B + y_O)) = (2/3, 1/3 * (m + 4)).
Để G thuộc đường thẳng 3x + 3y - 8 = 0, ta cần có 3 * (2/3) + 3 * (1/3 * (m + 4)) - 8 = 0. Giải phương trình này, ta được m = 2.
Vậy, đáp án là B. m = 2.
là y = -3;
Đáp án A