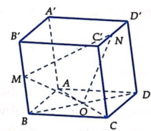
Cho hình hộp ABCD.A’B’C’D’, O , M, N lần lượt là trung điểm cuả Bb’ và C’D’. Mặt phẳng (MNO) cắt B’C’ tại E thì tỉ số B ' E E C ' là:
A. 7 5
B. 2 3
C. 1 3
D. 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


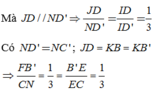

Đáp án C.
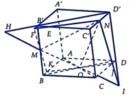
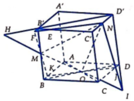
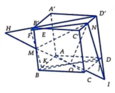
+ Trong mặt phẳng (BB’D’D) gọi I = MO ∩ DD', H = MO ∩ B'D'
Trong mặt phẳng (DD’C’C) gọi J = NI ∩ DC
Trong mặt phẳng (ABCD) gọi K = JO ∩ AB
Trong mặt phẳng (AA’B’B) gọi F = MK ∩ A'B'
Trong mặt phẳng (A’B’C’D’) gọi E = B'C' ∩ FN=> E = BC ∩ (MNO)
![]()
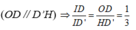
![]()
![]()
![]()

Đáp án C.
+ Trong mặt phẳng (BB’D’D) gọi I = M O ∩ DD ' , H = M O ∩ B ' D '
Trong mặt phẳng (DD’C’C) gọi J = N I ∩ D C
Trong mặt phẳng (ABCD) gọi K = J O ∩ A B
Trong mặt phẳng (AA’B’B) gọi F = M K ∩ A ' B '
Trong mặt phẳng (A’B’C’D’) gọi
E = B ' C ' ∩ F N ⇒ E = B C ∩ ( M N O )
BO = B’H = OD ⇒ C D H D ' = 1 3 (OD // D’H) ⇒ I D I D ' = O D H D ' = 1 3
Mà J D / / N D ' ⇒ J D N D ' = I D I D ' = 1 3
Có N D ' = N C '
J D = K B = K B ' ⇒ F B ' C N = 1 3 = B ' E E C = 1 3

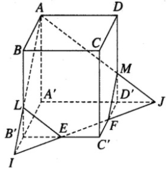
Giả sử đường thẳng EF cắt đường thẳng A’B’ tại I và cắt đường thẳng A’D’ tại J. AI cắt BB’ tại L, AJ cắt DD’ tại M. Gọi V0 là thể tích khối tứ diện AA’IJ. V là thể tích khối hộp ABCD.A’B’C’D’
Vì EB’ = EC’ và B’I // C’F
nên IB′ = FC′ = 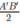
Do đó 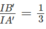
Để ý rằng BE’ // A’J , B’L // AA’
Ta có
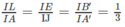
Từ đó suy ra:
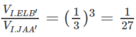
Do đó 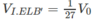
Tương tự 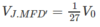
Gọi AB = a, BC = b , đường cao hạ từ A xuống (A’B’C’D’) là h thì
V = V ABCD . A ' B ' C ' D ' = h a b . sin ∠ BAD
![]()
Vậy
![]()
![]()
![]()

a)
Ta có: (ADD’A’) // (CBC’B’);
(ADD’A’) ∩ (DCB’A’) = A’D;
(CBC’B’) ∩ (DCB’A’) = B’C.
Do đó A’D // B’C, mà B’C ⊂ (B’CM) nên A’D // (B’CM).
Tương tự: (ABB’A’) // (DCC’D’);
(ABB’A’) ∩ (DMB’N) = MB’;
(DCC’D’) ∩ (DMB’N) = DN.
Do đó MB’ // DN, mà MB’ ⊂ (B’CM) nên DN // (B’CM).
Ta có: A’D // (B’CM);
DN // (B’CM);
A’D, DN cắt nhau tại điểm D và cùng nằm trong mp(A’DN)
Do đó (A’DN) // (B’CM).
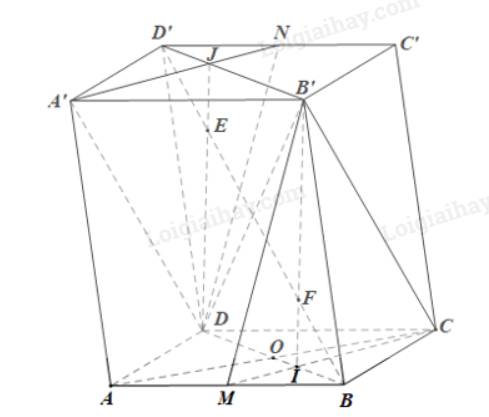
b)
Trong mp(A’B’C’D’), gọi J là giao điểm của A’N và B’D’.
Trong mp(BDD’B’), D’B cắt DJ tại E.
Ta có: D’B ∩ DJ = {E} mà DJ ⊂ (A’DN) nên E là giao điểm của D’B và (A’DN).
Tương tự, trong mp(ABCD), gọi I là giao điểm của CM và BD.
Trong mp(BDD’B’), D’B cắt B’I tại F.
Ta có: D’B ∩ B’I = {F} mà B’I ⊂ (B’CM) nên F là giao điểm của D’B và (B’CM).
• Ta có: (A’DN) // (B’CM);
(A’DN) ∩ (BDD’B’) = DJ;
(B’CM) ∩ (BDD’B’) = B’I.
Do đó DJ // B’I.
Trong mp(BDD’B’), xét DBDE có IF // DE nên theo định lí Thalès ta có: \(\frac{{BI}}{{BD}} = \frac{{BF}}{{BE}}\) (1)
Trong mp(ABCD), gọi O là giao điểm của hai đường chéo AC và BD trong hình bình hành ABCD. Khi đó O là trung điểm của AC, BD.
Xét ∆ABC, hai đường trung tuyến BO, CM cắt nhau tại I nên I là trọng tâm của tam giác
Suy ra \(\frac{{BI}}{{BO}} = \frac{2}{3}\) hay \(\frac{{BI}}{{\frac{1}{2}BD}} = \frac{{2BI}}{{BD}} = \frac{2}{3}\)
Do đó \(\frac{{BI}}{{BD}} = \frac{1}{3}\) (2)
Từ (1) và (2) suy ra \(\frac{{BF}}{{BE}} = \frac{1}{3}\)
Suy ra \(\frac{{D'E}}{{D'F - D'E}} = \frac{1}{{3 - 1}}\) hay \(\frac{{D'E}}{{EF}} = \frac{1}{2}\).
Chứng minh tương tự ta cũng có \(\frac{{D'E}}{{D'F}} = \frac{{D'J}}{{D'B'}} = \frac{1}{3}\)
Suy ra \(\frac{{D'E}}{{D'F - D'E}} = \frac{1}{{3 - 1}}\) hay \(\frac{{D'E}}{{EF}} = \frac{1}{2}\)
Do đó \(\frac{{BF}}{{EF}} = \frac{{D'E}}{{EF}} = \frac{1}{2}\) nên BF = D’E = ½ EF.

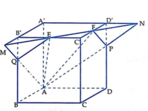
\( - \;\)Ta có \(\left( {ABB'C'} \right)\;//\;\left( {MNN'M'} \right),\;\left( {ADD'A'} \right) \cap \left( {ABB'A'} \right) = AA',\left( {ADD'A'} \right) \cap \left( {MNN'M'} \right) = MM'\)
suy ra AA'//MM'
Tương tự, BB' // NN'
ABNM.A'B'N'M' có các cạnh bên đôi một song song, (ABNM) //(A'B'N'M')
Suy ra ABNM.A'B'C'M' là hình lăng trụ.
\( - \;\)Ta có: \(\left( {ABB'C'} \right)\;//\;\left( {MNN'M'} \right),\;\left( {ABNM} \right) \cap \left( {ABB'A'} \right) = AB,\left( {ABNM} \right) \cap \left( {MNN'M'} \right) = MN\)
Suy ra AB//MN.
Ta có có AB // MN, BN// AM nên tứ giác ABNM là hình bình hành.
Do đó ABNM.A'B'C'M' là hình hộp.

Hướng dẫn: A
+ Đường cắt EF cắt A'D' tại N, M, AN cắt DD' tại P, AM cắt A'B' tại BB' tại Q. Từ đó mặt phẳng (AEF) cắt khối lăng trụ thành hai khối đó là ABCDC'QEFP và AQEFPB'A'D'.
+ Gọi
![]()
+ Do tính đối xứng của hình lập phương nên ta có V 4 = V 5
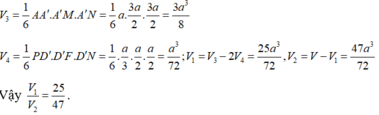

Chọn A
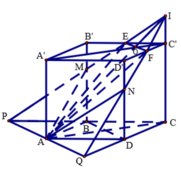
Dựng thiết diện: PQ qua A và song song với BD ( vì EF//B’D’//BD )
PE cắt các cạnh BB’, CC’ tại M và I. Tương tự ta tìm được giao điểm N. T iết diện là AMEFN.
Dựa vào đường trung bình BD và định lí Ta-lét cho các tam giác IAC, DNQ, D’NF ta tính được: I C ' = a 3 , N D = 2 a 3 Tương tự ta tính được: M B = 2 a 3
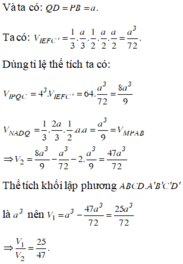

Đáp án A.
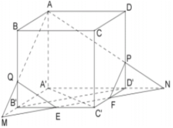
Đường thẳng EF cắt A'D' và A'B' tại N;M;AN cắt DD' tại P;AM cắt BB' tại Q. Khi đó thiết diện của hình lập phương khi cắt bởi mặt phẳng (AEF) là ngũ giác APFEQ
Từ giả thiết ta có V 1 = V A ' B ' D ' A P F E Q và V 2 = V A B C D C ' P F E Q ' .
Gọi
V = V A B C D . A ' B ' C ' D ' ; V 3 = V A . A ' M N ; V 4 = V P F D ' N ; V 5 = V Q M B ' E .
Do tính đối xứng của hình lập phương nên V 4 = V 5 .
Nhận thấy
V 3 = 1 6 A A ' . A ' M . A ' N = 1 6 . a . 3 a 2 . 3 a 2 = 3 a 2 8 (đvtt).
V 4 = 1 6 . D ' P . D ' F . D ' N = 1 6 . a 3 . a 2 . a 2 = a 3 72 (đvtt);
V 1 = V 3 − 2 V 4 = 3 a 3 8 − 2. a 3 72 = 25 a 3 72 (đvtt).
V 2 = V − V 1 = a 3 − 25 a 3 72 = 47 a 3 72 (đvtt).
Vậy V 1 V 2 = 25 47 .