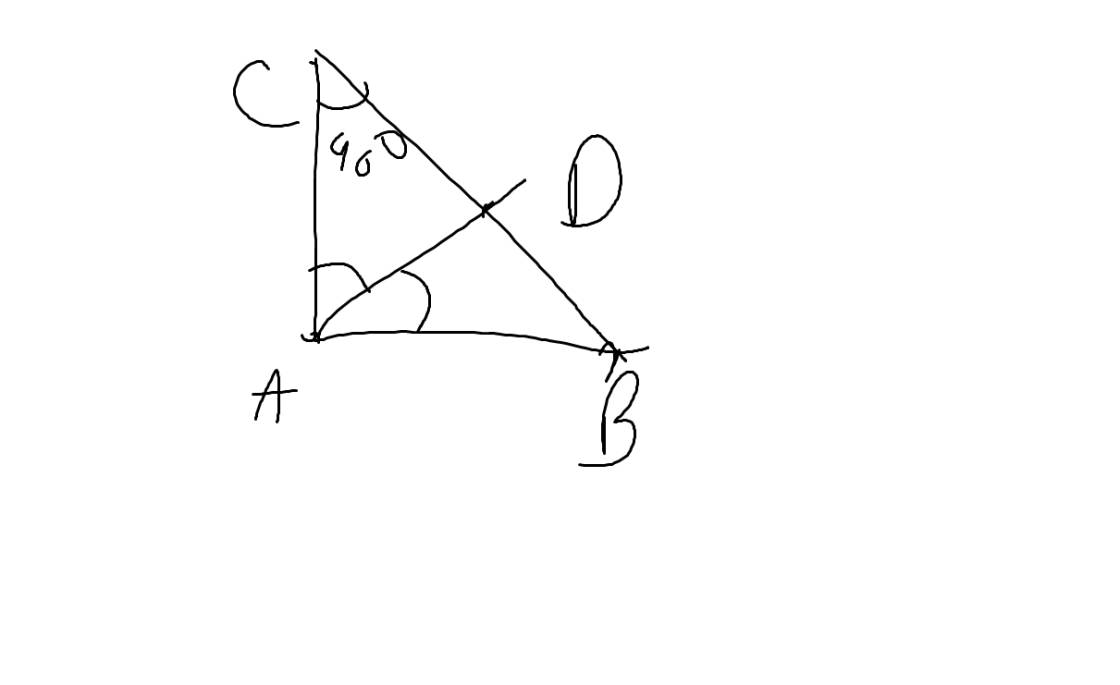
Cho tam giác ABC.Tia phân giác của góc A cắt BC tại D.Tính các góc của tam giác ABC,biết ADB=80o,B=1,5C
Giúp mik với ngày mai mik cần phải nộp bài cho cô!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
24 tháng 9 2021
Tam giác ABC có:
góc BAC + góc B + góc C = 180 độ
=> góc BAC + 80 độ + 30 độ = 180 độ
=> góc BAC = 180 độ - ( 80 độ + 30 độ) =70 độ
Vì AD là tia phân giác của góc BAC nên:
góc BAD = góc BAC / 2 = 70/2 = 35 độ
Vì góc ADC là góc ngoài của tam giác ADB nên:
góc ADC = góc B + góc BAD
= 80 độ + 35 độ =115 độ
Ta có: góc ADB + góc ADC = 180 độ ( kề bù)
=> góc ADB = 180 độ - góc ADC
= 180 độ - 115 độ = 65 độ
Vậy góc ADC = 115 độ, góc ADB = 65 độ
chúc em học tốt !
22 tháng 12 2021
a: Xét ΔAKB và ΔAKC có
AK chung
KB=KC
AB=AC
Do đó: ΔAKB=ΔAKC
CM
28 tháng 3 2019
Ta có AD là tia phân giác của ∠(BAC) nên ∠(BAD) = 32o
Trong tam giác ABD có ∠(ADB) = 180o - 32o - 80o = 68o. Chọn C
23 tháng 11 2023
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}+40^0=90^0\)
=>\(\widehat{ABC}=50^0\)
AD là phân giác của góc BAC
=>\(\widehat{BAD}=\widehat{CAD}=\dfrac{\widehat{BAC}}{2}=\dfrac{90^0}{2}=45^0\)
Xét ΔADB có \(\widehat{ADC}\) là góc ngoài tại đỉnh D
nên \(\widehat{ADC}=\widehat{DAB}+\widehat{ABD}=45^0+50^0=95^0\)
\(\widehat{ADB}+\widehat{ADC}=180^0\)(hai góc kề bù)
=>\(\widehat{ADB}+95^0=180^0\)
=>\(\widehat{ADB}=85^0\)
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Lời giải:
Do $AD$ là phân giác $\widehat{A}$ nên $\widehat{DAC}=\widehat{DAB}$
Ta có:
$\widehat{ADB}=\widehat{DAC}+\widehat{C}$
$\widehat{ADC}=\widehat{DAB}+\widehat{B}$
$\Rightarrow \widehat{ADC}-\widehat{ADB}=\widehat{B}-\widehat{C}=\alpha$
Mà $\widehat{ADC}+\widehat{ADB}=180^0$
Do đó:
$\widehat{ADC}=\frac{180^0+\alpha}{2}$
$\widehat{ADB}=\frac{180^0-\alpha}{2}$
AH
Akai Haruma
Giáo viên
12 tháng 7 2021
Minz Ank: à đó là tính chất góc kề bù 1 góc trong tam giác thì bằng tổng 2 góc còn lại trong tam giác đó.
Dễ hiểu hơn, thì trong tam giác $ADC$ chả hạn, tổng 3 góc $\widehat{ADC}+\widehat{DAC}+\widehat{C}=180^0$
Mà $\widehat{ADC}+\widehat{ADB}=180^0$
$\Rightarrow \widehat{DAC}+\widehat{C}=\widehat{ADB}$ đó em