Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Câu 1:
a; \(\dfrac{-9}{4}\) < 0; \(\dfrac{1}{3}\) > o
\(\dfrac{-9}{4}\) < \(\dfrac{1}{3}\)
b; \(\dfrac{-8}{3}\) < - 1
\(\dfrac{4}{-7}\) > - 1
Vậy \(\dfrac{-8}{3}\) < \(\dfrac{4}{-7}\)
c; \(\dfrac{9}{-5}\) < - 1
\(\dfrac{7}{-10}\) > - 1
Vậy \(\dfrac{9}{-5}\) < \(\dfrac{7}{-10}\)
Câu 2:
a; Viết các phân số theo thứ tự tăng dần
\(\dfrac{-1}{2}\); \(\dfrac{2}{7}\); \(\dfrac{2}{5}\)
b; \(\dfrac{-11}{4}\); \(\dfrac{-7}{3}\); \(\dfrac{12}{5}\)

\(8,\\ A=\left\{0;1;2;3\right\}\\ B=\left\{0;1;2\right\}\\ A\cap B=\left\{0;1;2\right\}\\ A\cup B=\left\{0;1;2;3\right\}\\ A\B=\left\{3\right\}\\ B\A=\varnothing\\ 9,\\ A=\left\{0;1;2;3;4\right\}\\ B=\left\{5;6\right\}\\ A\cap B=\varnothing\\ A\cup B=\left\{0;1;2;3;4;5;6\right\}\\ A\B=\left\{0;1;2;3;4\right\}\\ B\A=\left\{5;6\right\}\)

a) \(\sqrt{4-2\sqrt{3}}=\sqrt{3}-1\)
b) \(\sqrt{9-4\sqrt{5}}=\sqrt{10}-1\)
c) \(\sqrt{12+6\sqrt{3}}=3+\sqrt{3}\)
d) \(\sqrt{30-12\sqrt{6}}=3\sqrt{2}-2\sqrt{3}\)
e) \(\sqrt{8-\sqrt{60}}=\sqrt{5}-\sqrt{3}\)
f) \(\sqrt{-\sqrt{96}+25}=2\sqrt{6}-1\)


5:
Chiều rộng là (36-6):2=15(m)
Chiều dài là 15+6=21m
S=15*21=315m2

\(y'=\dfrac{\left(-2x+2\right)\left(x-3\right)-\left(-x^2+2x+c\right)}{\left(x-3\right)^2}=\dfrac{-x^2+6x-6-c}{\left(x-3\right)^2}\)
\(\Rightarrow\) Cực đại và cực tiểu của hàm là nghiệm của: \(-x^2+6x-6-c=0\) (1)
\(\Delta'=9-\left(6+c\right)>0\Rightarrow c< 3\)
Gọi \(x_1;x_2\) là 2 nghiệm của (1) \(\Rightarrow\left\{{}\begin{matrix}-x_1^2+6x_1-6=c\\-x_2^2+6x_2-6=c\end{matrix}\right.\)
\(\Rightarrow m-M=\dfrac{-x_1^2+2x_1+c}{x_1-3}-\dfrac{-x_2^2+2x_2+c}{x_2-3}=4\)
\(\Leftrightarrow\dfrac{-2x_1^2+8x_1-6}{x_1-3}-\dfrac{-2x_2^2+8x_2-6}{x_2-3}=4\)
\(\Leftrightarrow2\left(1-x_1\right)-2\left(1-x_2\right)=4\)
\(\Leftrightarrow x_2-x_1=2\)
Kết hợp với Viet: \(\left\{{}\begin{matrix}x_2-x_1=2\\x_1+x_2=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=2\\x_2=4\end{matrix}\right.\)
\(\Rightarrow c=2\)
Có 1 giá trị nguyên

10. Câu này chứng minh BĐT BSC:
\(\sqrt{\left(a^2+b^2\right)\left(b^2+c^2\right)}\ge\sqrt{\left(ab+bc\right)^2}=b\left(a+c\right)\)
11.
Ta có: \(\dfrac{1}{1+a}+\dfrac{1}{1+b}-\dfrac{2}{1+\sqrt{ab}}\)
\(=\dfrac{\left(1+b\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{\left(1+a\right)\left(1+\sqrt{ab}\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2\left(1+a\right)\left(1+b\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{1+b+\sqrt{ab}+b\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}+\dfrac{1+a+\sqrt{ab}+a\sqrt{ab}}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}-\dfrac{2+2a+2b+2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{-a-b+2\sqrt{ab}+a\sqrt{ab}+b\sqrt{ab}-2ab}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\)
\(=\dfrac{\left(\sqrt{a}-\sqrt{b}\right)^2\left(\sqrt{ab}-1\right)}{\left(1+a\right)\left(1+b\right)\left(1+\sqrt{ab}\right)}\ge0\forall x,y\ge1\)
Đẳng thức xảy ra khi \(a=b=1\)

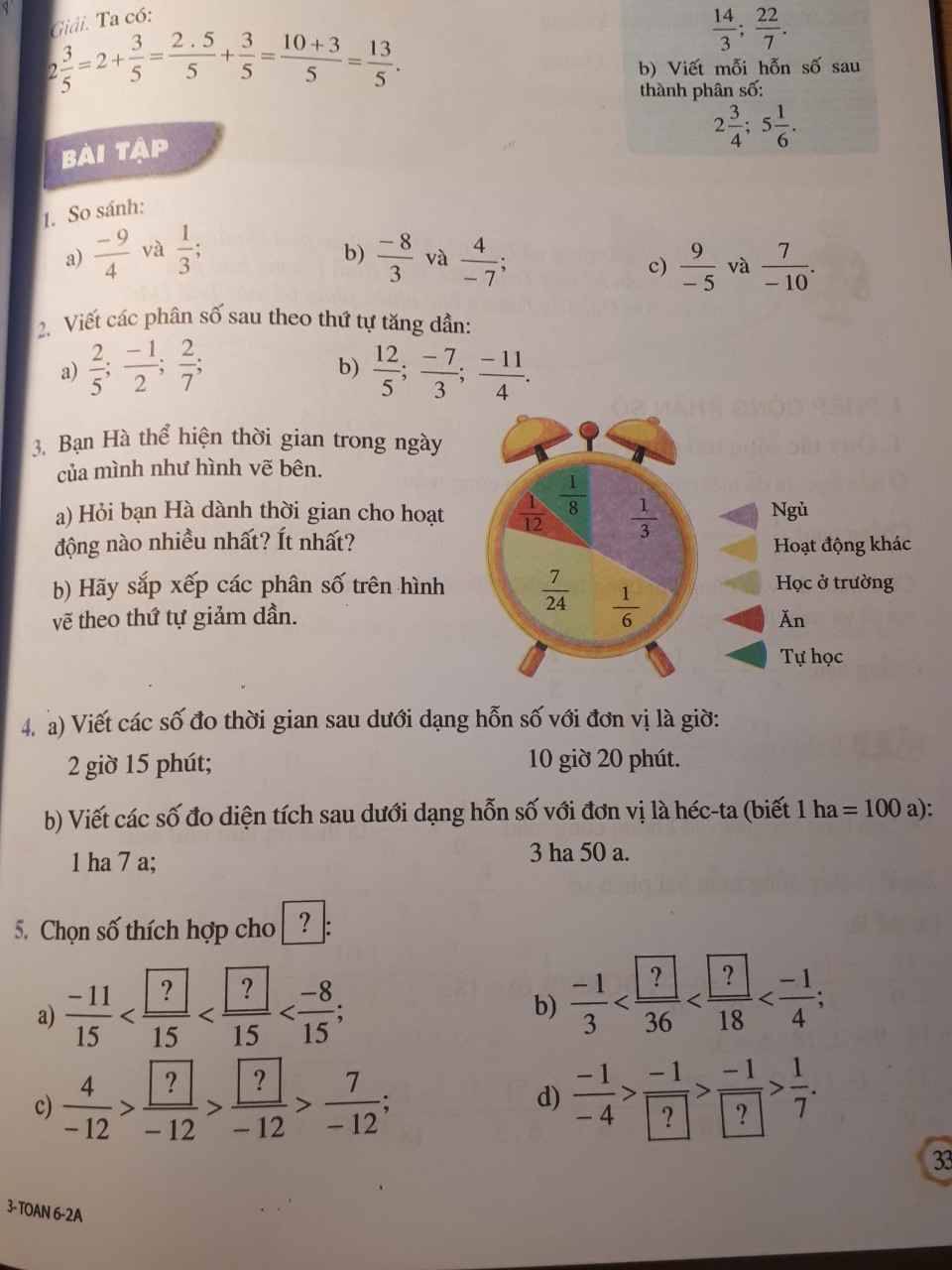
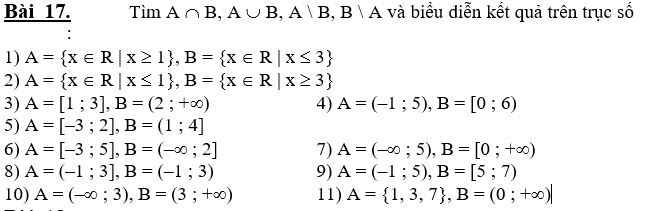
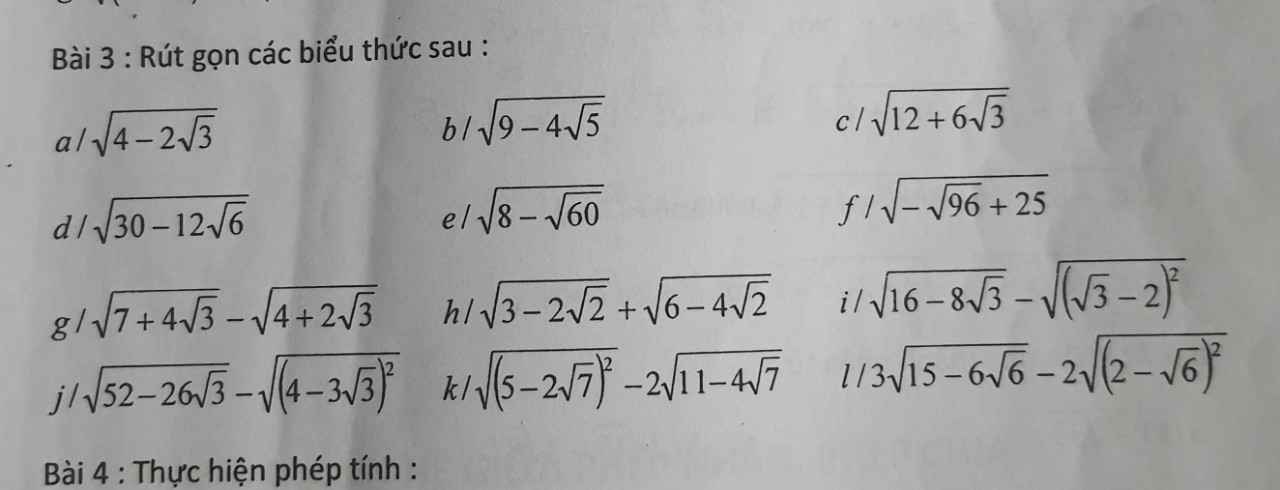



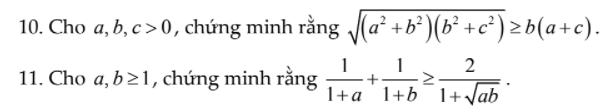 !
!