Tìm x biết :
a) x3 - 3x2 - 4x + 12 = 0
b) x2 - 7x + 10 = 0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
Bài 1.
28 tháng 2 2021
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
28 tháng 2 2021
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
25 tháng 10 2021
\(a,\Leftrightarrow\left(4x-8\right)\left(x+1\right)=0\\ \Leftrightarrow4\left(x-2\right)\left(x+1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\\ b,\Leftrightarrow\left(x+1\right)\left(x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x^2=-1\left(vô.lí\right)\end{matrix}\right.\Leftrightarrow x=-1\\ c,\Leftrightarrow x^2-2x-4x+8=0\\ \Leftrightarrow\left(x-2\right)\left(x-4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=4\end{matrix}\right.\\ d,\Leftrightarrow x^3-3x^2+3x-9x+2x-6=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x^2+x+2x+2\right)=0\\ \Leftrightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-1\\x=-2\end{matrix}\right.\)
25 tháng 10 2021
a) \(\Rightarrow4\left(x+1\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=-1\\x=2\end{matrix}\right.\)
b) \(\Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\)
\(\Rightarrow\left(x+1\right)\left(x^2+1\right)=0\)
\(\Rightarrow x=-1\left(do.x^2+1\ge1>0\right)\)
c) \(\Rightarrow x\left(x-4\right)-2\left(x-4\right)=0\)
\(\Rightarrow\left(x-4\right)\left(x-2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)
d) \(\Rightarrow x^2\left(x-3\right)+3x\left(x-3\right)+2\left(x-3\right)\)
\(\Rightarrow\left(x-3\right)\left(x^2+3x+2\right)=0\)
\(\Rightarrow\left(x-3\right)\left(x+1\right)\left(x+2\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-2\\x=-1\end{matrix}\right.\)
CM
2 tháng 7 2017
a) 3 x 2 − 7 x − 10 ⋅ 2 x 2 + ( 1 − 5 ) x + 5 − 3 = 0
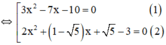
+ Giải (1):
3 x 2 – 7 x – 10 = 0
Có a = 3; b = -7; c = -10
⇒ a – b + c = 0
⇒ (1) có hai nghiệm x 1 = - 1 v à x 2 = - c / a = 10 / 3 .
+ Giải (2):
2 x 2 + ( 1 - √ 5 ) x + √ 5 - 3 = 0
Có a = 2; b = 1 - √5; c = √5 - 3
⇒ a + b + c = 0
⇒ (2) có hai nghiệm:
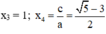
Vậy phương trình có tập nghiệm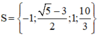 
b)
x 3 + 3 x 2 - 2 x - 6 = 0 ⇔ x 3 + 3 x 2 - ( 2 x + 6 ) = 0 ⇔ x 2 ( x + 3 ) - 2 ( x + 3 ) = 0 ⇔ x 2 - 2 ( x + 3 ) = 0
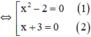
+ Giải (1): x 2 – 2 = 0 ⇔ x 2 = 2 ⇔ x = √2 hoặc x = -√2.
+ Giải (2): x + 3 = 0 ⇔ x = -3.
Vậy phương trình có tập nghiệm S = {-3; -√2; √2}
c)
x 2 − 1 ( 0 , 6 x + 1 ) = 0 , 6 x 2 + x ⇔ x 2 − 1 ( 0 , 6 x + 1 ) = x ⋅ ( 0 , 6 x + 1 ) ⇔ x 2 − 1 ( 0 , 6 x + 1 ) − x ( 0 , 6 x + 1 ) = 0 ⇔ ( 0 , 6 x + 1 ) x 2 − 1 − x = 0
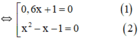
+ Giải (1): 0,6x + 1 = 0 ⇔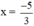 
+ Giải (2):
x 2 – x – 1 = 0
Có a = 1; b = -1; c = -1
⇒ Δ = ( - 1 ) 2 – 4 . 1 . ( - 1 ) = 5 > 0
⇒ (2) có hai nghiệm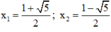 
Vậy phương trình có tập nghiệm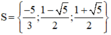 
d)
x 2 + 2 x − 5 2 = x 2 − x + 5 2 ⇔ x 2 + 2 x − 5 2 − x 2 − x + 5 2 = 0 ⇔ x 2 + 2 x − 5 − x 2 − x + 5 ⋅ x 2 + 2 x − 5 + x 2 − x + 5 = 0 ⇔ ( 3 x − 10 ) 2 x 2 + x = 0
⇔ (3x-10).x.(2x+1)=0
+ Giải (1): 3x – 10 = 0 ⇔ 
+ Giải (2):
9 tháng 10 2021
1)
a) \(=15x^3-20x^2+10x\)
b) \(=3x^4-x^3+4x^2-9x^3+3x-12x=3x^4-10x^3+4x^2-9x\)
2)
a) \(\Rightarrow x\left(x^2-6x+12\right)=0\)
\(\Rightarrow x=0\)(do \(x^2-6x+12=\left(x^2-6x+\dfrac{36}{4}\right)+3=\left(x-\dfrac{6}{2}\right)^2+3\ge3>0\))
b) \(\Rightarrow\left(x+3\right)^3=0\Rightarrow x=-3\)
23 tháng 3 2022
(3x²-5x+2)+(3x²+5x)= bao nhiêu ạ
Giúp em vs ạ . Em cảm ơn
RH
2 tháng 10 2021
2a) pt <=> (x + 6)^2 = 0
<=> x = -6
b) pt <=> (4x - 1)^2 = 0
<=> x = 1/4
c) pt<=> (x + 1)^3 = 0
<=> x = -1
2 tháng 10 2021
Bài 1:
a: Ta có: \(A=\left(4x+3y\right)^2+\left(4x-3y\right)^2\)
\(=16x^2+24xy+9y^2+16x^2-24xy+9y^2\)
\(=32x^2+18y^2\)
b: Ta có: \(B=\left(x-2\right)^3-\left(x+2\right)^3\)
\(=x^3-6x^2+12x-8-x^3-6x^2-12x-8\)
\(=-12x^2-24\)
2 tháng 10 2021
Bài 2:
a: Ta có: \(x^2+12x+36=0\)
\(\Leftrightarrow x+6=0\)
hay x=-6
b: Ta có: \(16x^2-8x+1=0\)
\(\Leftrightarrow4x-1=0\)
hay \(x=\dfrac{1}{4}\)
2 tháng 10 2021
Bài 1:
a: Ta có: \(A=\left(4x+3y\right)^2+\left(4x-3y\right)^2\)
\(=16x^2+24xy+9y^2+16x^2-24xy+9y^2\)
\(=32x^2+18y^2\)
b: Ta có: \(B=\left(x-2\right)^3-\left(x+2\right)^3\)
\(=x^3-6x^2+12x-8-x^3-6x^2-12x-8\)
\(=-12x^2-24\)
c: Ta có: \(C=\left(x+2y\right)^2+2\left(x+2y\right)\left(x-2y\right)+\left(x-2y\right)^2\)
\(=\left(x+2y+x-2y\right)^2\)
\(=4x^2\)
TH
1
20 tháng 10 2021
\(a,\Leftrightarrow\left(x-4\right)\left(x^2+5\right)>0\\ \Leftrightarrow x-4>0\left(x^2+5\ge5>0\right)\\ \Leftrightarrow x>4\\ b,\Leftrightarrow\left(x-y\right)\left(3x-5\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=y\left(vô.lí.do.x\ne y\right)\\x=\dfrac{5}{3}\left(tm\right)\end{matrix}\right.\\ \Leftrightarrow S=x^2-x=\dfrac{25}{9}-\dfrac{5}{3}=\dfrac{10}{9}\)
thêm câu b, x2-7x+10
=x2-2x-5x+10
=(x2-2x)-(5x+10)
= x(x-2)-5(x+2)
=(x-2)(x-5)