Cho ΔABC nhọn, kẻ đường cao BD và CE, vẽ các đường cao DF và EG của ΔADE. ΔABD đồng dạng với tam giác nào dưới đây?
A. ΔAEG
B. ΔABC
C. Cả A và B
D. Không có tam giác nào
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có: A E A B = A G A D = E G B D
=> ΔAEG ~ ΔABD (c - c - c) nên (1) đúng.
Tương tự ta cũng chứng minh được ΔADF ~ ΔACE nên (2) đúng
Dễ thấy (3) sai vì A E A B ≠ A C A C
Vậy có hai cặp tam giác đồng dạng trong các cặp đã nêu.
Đáp án: C

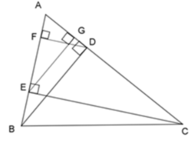
Từ câu trước ta có: A E A B = A G A D = E G B D => AE.AD = AB.AG (1) nên A đúng
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> A F A E = A D A C => AF.AC = AE.AD (2) nên B đúng
Ngoài ra A D A C = F D E C => AD.EC = AC.FD nên C đúng
Chỉ có đáp án D sai vì A E E G = A B B D
Đáp án: D

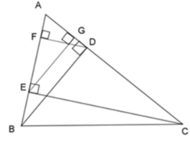
Từ câu trước ta có: A E A B = A G A D => AE.AD = AB.AG (1)
Chứng minh tương tự, ta được: ΔAFD ~ ΔAEC (c - c - c)
=> => AF.AC = AE.AD (2)
Từ (1) và (2) ta có: AD.AE = AB.AG = AC.AF
Đáp án: B

Hình Tự Vẽ
Xét \(\Delta AEC\)và \(\Delta ADB\)có :\(\widehat{A}\)chung :\(\widehat{E}\)=\(\widehat{D}\)\(\Rightarrow\)\(\Delta AEC\)\(\approx\)\(\Delta ADB\)\(\Rightarrow\)\(\widehat{ABD}\)=\(\widehat{ACE}\)
Xét \(\Delta HDC\)và \(\Delta HEB\)có : \(\widehat{D}\)=\(\widehat{C}\); \(\widehat{HCD}\)=\(\widehat{HBE}\)\(\Rightarrow\)\(\Delta HDC\)\(\approx\)\(\Delta HEB\)\(\Rightarrow\)\(\frac{HB}{HC}\)= \(\frac{HE}{HD}\)\(\Rightarrow\)HB.HD=HC.HE
a) Xét tam giác ADB và tam giác AEC có:
Chung DAB; 2 góc vuông ADB=AEC=90 độ (có 2 đường cao BD, CE lần lượt hạ từ B; C xuống)
=> Đồng dạng theo TH gg
b; c) Có: BEC=BDC=90 độ
=> Tứ giác BCDE nội tiếp
=> góc HDE= góc ECB (tính chất)
=> tam giác HDE đồng dạng tam giác HCB (gg)
=> \(\frac{HD}{HE}=\frac{HC}{HB}\)
=> \(HD.HB=HC.HE\)(ĐPCM)
d) Xét tứ giác ADHE có: góc ADH=góc AEH=90 độ
=> góc ADH + góc AEH=90+90=180 độ
=> Tứ giác ADHE nội tiếp
=> góc AHD=góc AED (tính chất) (*)
Có tứ giác BCDE nội tiếp (cmt) => góc AED=góc ACB (tính chất) (**)
Từ (*) và (**) => góc ACB=góc AHD.
=> Tam giác DHA đồng dạng tam giác DCB (gg) khi có \(\hept{\begin{cases}ACB=AHD\left(cmt\right)\\ADH=BCD=90\end{cases}}\)
=> \(\frac{DH}{DA}=\frac{DC}{DB}\)
=> \(DH.DB=DA.DC\)(ĐPCM)
e) Đề bài sai nhé (CM đồng dạng chứ ko phải là CM bằng nhau)
Có: góc AED=góc ACB (cmt)
Và có chung góc DAE
=> Tam giác ADE đồng dạng tam giác ACB (gg)
=> ĐPCM

a, Xét tam giác ABD và tam giác ACE
^A _ chung
^ADB = ^AEC = 900
Vậy tam giác ABD ~ tam giác ACE (g.g)
b, Xét tam giác CBD và tam giác CAK ta có
^C _ chung
^CDB = ^CKA = 900
Vậy tam giác CDB ~ tam giác CKA (g.g)
\(\dfrac{CD}{CK}=\dfrac{CB}{CA}\Rightarrow CD.CA=CB.CK\)
c, Xét tam giác KDC và tam giác ABC
^C _ chung
\(\dfrac{DC}{BC}=\dfrac{KC}{AC}\)( tỉ lệ thức tỉ số đồng dạng )
Vậy tam giác KDC ~ tam giác ABC (c.g.c)

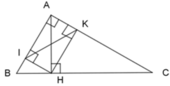
Gọi I, K lần lượt là hình chiếu của H lên AB và AC.
⇒ H I A ^ = H K A ^ = 90 ∘
Xét tứ giác AIHK có: I A K ^ = H I A ^ = H K A ^ = 90 ∘
=> Tứ giác AIHK là hình chữ nhật (dhnb)
+) Xét ΔAIK và ΔIAH ta có:
AI chung
AK = IH (theo tính chất của hình chữ nhật)
AH = IK (theo tính chất của hình chữ nhật)
=> ΔAIK = ΔIAH (c - c - c) (1)
Xét 2 tam giác vuông ΔIAH và ΔHAB có: A chung
=> ΔIAH ~ ΔHAB (g - g) (2)
Xét 2 tam giác vuông ΔHAB và ΔACB có: B chung
=> ΔHAB ~ ΔACB (g - g) (3)
Từ (1), (2) và (3) ta có: ΔAIK ~ ΔACB
Đáp án: A
Xét ΔABD và ΔAEG, ta có:
BD ⊥ AC (BD là đường cao)
EG ⊥ AC (EG là đường cao)
=> BD // EG
Theo định lý Talet, ta có: A E A B = A G A D = E G B D
=> ΔAEG đồng dạng ΔABD (c - c - c) (đpcm)
Đáp án: A