Cho tam giác ABC. Các điểm D, E, F theo thứ tự làm trung điểm của BC, CA, AB. Các điểm A’, B’, C’ theo thứ tự là trung điểm của EF, DF, DE. Chọn câu đúng?
A. ΔA’B’C’ đồng dạng ΔABC theo tỉ số k = 1 2
B. ΔEDF đồng dạng ΔABC theo tỉ số k = 1 2
C. ΔA’B’C’ đồng dạng ΔABC theo tỉ số k = 1 4
D. ΔA’B’C’ đồng dạng ΔEDF theo tỉ số k = 1 2

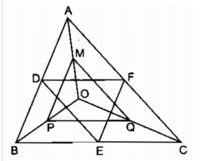
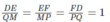


Vì D, E, F theo thứ tự làm trung điểm của BC, CA, AB nên EF, ED, FD là các đường trung bình của tam giác ABC nên E F B C = F D A C = E D A B = 1 2 suy ra ΔABC ~ ΔDEF (c - c - c) theo tỉ số đồng dạng k = 2.
Tương tự ta có A’B’, B’C’, C’A’ là các đường trung bình của tam giác DEF nên ΔA’B’C’ đồng dạng ΔDEF theo tỉ số k = 1 2
Theo tính chất đường trung bình B ' C E F = 1 2 mà E F B C = 1 2 (cmt) suy ra B ' C ' B C = 1 4
Tương tự A ' B ' A B = A ' C ' A C = 1 4
Do đó ΔA’B’C’ đồng dạng ΔABC theo tỉ số k = 1 4
Đáp án: C