Chọn phát biểu đúng: Phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có a – b + c = 0. Khi đó:
A. Phương trình có một nghiệm x 1 = 1 , nghiệm kia là x 2 = c a
B. Phương trình có một nghiệm x 1 = − 1 , nghiệm kia là x 2 = c a
C. Phương trình có một nghiệm x 1 = − 1 , nghiệm kia là x 2 = - c a
D. Phương trình có một nghiệm x 1 = 1 , nghiệm kia là x 2 = - c a

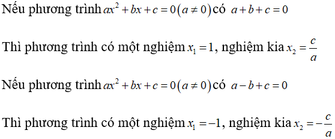
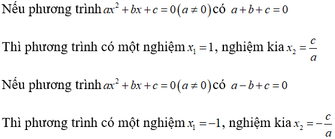
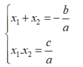
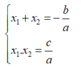
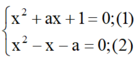
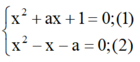
+) Nếu phương trình a x 2 + b x c = 0 ( a ≠ 0 ) có a + b + c = 0 thì phương trình có một nghiệm x 1 = 1 , nghiệm kia là x 2 = c a
+) Nếu phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có a − b + c = 0 thì phương trình có một nghiệm x 1 = − 1 , nghiệm kia là x 2 = − c a
Đáp án: C