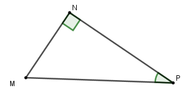
Cho tam giác MNP vuông tại N. Hệ thức nào sau đây là đúng?
A. NP = MP. sin P
B. NP = MN. cot P
C. NP = MN. tan P
D. NP = MP. cot P
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

hc tốt nha
câuA ha
Vì tam giác MNP là tam giác đều, nên độ dài các cạnh MN, NP và MP sẽ bằng nhau. Do đó, khẳng định A là đúng vì MN bằng MP.

a: NP^2=MN^2+MP^2
=>ΔMNP vuông tại M
b: Xét ΔNMD vuông tại M và ΔNED vuông tại E có
ND chung
góc MND=góc END
=>ΔNMD=ΔNED
=>DM=DE

a: ta có: ΔMNP cân tại M
mà MH là đường cao
nên H là trung điểm của NP
hay HN=HP
b: NH=NP/2=8/2=4(cm)
=>MH=3(cm)
c: Xét ΔMDH vuông tại D và ΔMEH vuông tại E có
MH chung
\(\widehat{DMH}=\widehat{EMH}\)
Do đó: ΔMDH=ΔMEH
Suy ra: HD=HE
hay ΔHED cân tại H

Ta có: \(\widehat{N}\)+\(\widehat{M}\)+\(\widehat{P}\)= 1800 ( ĐL)
\(\Rightarrow60^o+\widehat{M}+40^o\)\(=180^0\)
\(\Rightarrow\widehat{M}=180^0-\left(60^0+40^0\right)\)
\(\Rightarrow\)\(\widehat{M}\)\(=180^0-100^0\)
\(\Rightarrow\widehat{M}=80^0\)
Áp dụng ĐL ta có
\(\widehat{N}\)đối diện với cạnh \(MP\)
\(\widehat{M}\)đối diện với cạnh \(NP\)
\(\widehat{P}\)đối diện với cạnh \(MN\)
Mà\(\widehat{P}\)\(< \) \(\widehat{N}\)\(< \)\(\widehat{M}\)
\(\Rightarrow\)MN<MP<NP (ĐPCM)
Ta có cot P = N P M N => NP = MN. cot P
Đáp án cần chọn là: B