Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Phương trình 5 x 2 + 21x − 36 = 0 có a + b + c = 5 +21 – 26 = 0 nên phương trình có hai nghiệm phân biệt là x 1 = 1 ; x 2 = - 26 5 . Khi đó B = 5. (x − 1) x + 26 5
Đáp án: C
\(a,5\left(x-y\right)-3x\left(y-x\right)=5\left(x-y\right)+3x\left(x-y\right)=\left(5+3x\right)\left(x-y\right)\\ b,x^2-4xy+4y^2=\left(x-2y\right)^2\\ c,\left(x+1\right)^2+x\left(5-x\right)=0\\ \Rightarrow x^2+2x+1+5x-x^2=0\\ \Rightarrow7x+1=0\\ \Rightarrow7x=-1\\ \Rightarrow x=-\dfrac{1}{7}\)
a: =(x-y)(5+3x)
c: \(\Leftrightarrow x^2-2x+1+5x-x^2=0\)
hay x=-1/3
Bài 1 :
\(49\left(x-2\right)^2-25\left(2x+1\right)^2=0\)
\(\Leftrightarrow\left[7\left(x-2\right)-5\left(2x+1\right)\right]\left[7\left(x-2\right)+5\left(2x+1\right)\right]=0\)
\(\Leftrightarrow\left(7x-14-10x-5\right)\left(7x-14+10x+5\right)=0\)
\(\Leftrightarrow\left(-3x-19\right)\left(17x-9\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}-3x=19\\17x=9\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-19}{3}\\x=\frac{9}{17}\end{cases}}}\)
Bài 2 :
+) \(9x^2-6xy+y^2-21x+7y\)
\(=\left(3x-y\right)^2-7\left(3x-y\right)\)
\(=\left(3x-y\right)\left(3x-y-7\right)\)
+) \(x^2+2x-35\)
\(=x^2+2x+1-36\)
\(=\left(x+1-6\right)\left(x+1+6\right)\)
\(=\left(x-5\right)\left(x+7\right)\)
+) \(2x^2+9x-5\)
\(=2x^2-x+10x-5\)
\(=x\left(2x-1\right)+5\left(2x-1\right)\)
\(=\left(2x-1\right)\left(x+5\right)\)
+) \(6x^2+23x+15\)
\(=6x^2+18x+5x+15\)
\(=6x\left(x+3\right)+5\left(x+3\right)\)
\(=\left(x+3\right)\left(6x+5\right)\)
a)\(2x^2-12x=-18\)
\(\Leftrightarrow2x^2-12x+18=0\)
\(\Leftrightarrow2\left(x^2-6x+9\right)=0\)
\(\Leftrightarrow2\left(x-3\right)^2=0\)
\(\Leftrightarrow\left(x-3\right)^2=0\)
\(\Leftrightarrow x-3=0\)
\(\Leftrightarrow x=3\)
b) \(\left(4x^2-4x+1\right)-x^2=0\)
\(\Leftrightarrow\left(2x-1\right)^2-x^2=0\)
\(\Leftrightarrow\left(2x-1-x\right)\left(2x-1+x\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-1=0\\3x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=1\\x=\frac{1}{3}\end{cases}}}\)
_Minh ngụy_
\(x^2-ay-y^2-ax\)
\(=\left(x^2-y^2\right)-\left(ax+ay\right)\)
\(=\left(x-y\right)\left(x+y\right)-a\left(x+y\right)\)
\(=\left(x+y\right)\left(x-y-a\right)\)
_Minh ngụy_
a) Thay x = 3 2 vào (1) và (2) thấy thỏa mãn nên x = 3 2 là nghiệm chung của cả hai PT đã cho.
b) Thay x = -5 vào (2) thấy thỏa mãn nên x = -5 là nghiệm của (2). Thay x = -5 vào (1) thấy không thỏa mãn nên x = -5 không là nghiệm của (1).
c) Cách 1. Tìm được tập nghiệm của (1) và (2) lần lượt là S 1 = { 1 ; 3 2 } và S 2 = { - 5 ; 3 2 }
Vì S 1 ≠ S 2 Þ Hai phương trình không tương đương nhau.
Cách 2. Theo ý b, x = -5 là nghiệm của (2) nhưng không là nghiệm của (1) nên hai PT không có cùng tập nghiệm.
a: \(=9-4\sqrt{5}\cdot\dfrac{1}{\sqrt{5}}=9-4=5\)
b: \(=\sqrt{5}-2-\dfrac{1}{2}\cdot2\sqrt{5}=-2\)
3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:
\(A=x^3+9x^2+23x+15=x^2\left(x+1\right)+8x\left(x+1\right)+15\left(x+1\right)\)
\(=\left(x+1\right)\left(x^2+8x+15\right)=\left(x+1\right)\left[x\left(x+3\right)+5\left(x+3\right)\right]\)
\(=\left(x+1\right)\left(x+3\right)\left(x+5\right)⋮16\)
b, Nếu x là số chẵn thì A là số lẻ nên không chia hết cho 16
- Nếu x là số lẻ thì đặt x = 2k + 1 \(\left(k\in Z\right)\)
Ta có: \(A=\left(x+1\right)\left(x+3\right)\left(x+5\right)=\left(2k+1+1\right)\left(2k+1+3\right)\left(2k+1+5\right)\)
\(=\left(2k+2\right)\left(2k+4\right)\left(2k+6\right)=8\left(k+1\right)\left(k+2\right)\left(k+3\right)\)
Vì k + 1, k + 2 và k + 3 là 3 số nguyên liên tiếp nên
\(\left(k+1\right)\left(k+2\right)\left(k+3\right)⋮2\Rightarrow A=8\left(k+1\right)\left(k+2\right)\left(k+3\right)⋮16\)
Vậy với x là số lẻ \(\left(x\in Z\right)\) thì \(A⋮16\)
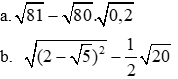
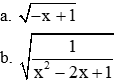
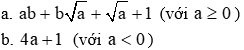
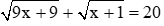
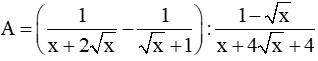
Phương trình 18 x 2 + 23x + 5 = 0 có a – b + c = 18 – 23 + 5 = 0 nên phương trình có hai nghiệm phân biệt là x 1 = − 1 ; x 2 = − 5 18 . Khi đó A = 18 (x + 1) x + 5 18
Đáp án: A