Chọn khẳng định đúng. Nếu phương trình a x 2 = m . x + n có hai nghiệm phân biệt thì đường thẳng d: y = mx + n và parabol (P): y = a x 2
A. Cắt nhau tại hai điểm
B. Tiếp xúc với nhau
C. Không cắt nhau
D. Cắt nhau tại gốc tọa độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 không cắt nhau thì phương trình a x 2 = m x + n vô nghiệm.

Đường thẳng d: y = mx + n và parabol (P): y = a x 2 không cắt nhau khi phương trình a x 2 = m . x + n vô nghiệm
Đáp án: C

a: Thay x=1 vào (P), ta được:
y=1^2=1
Thay x=1 và y=1 vào (d), ta được:
m+n=1
=>m=1-n
PTHĐGĐ là:
x^2-mx-n=0
=>x^2-x(1-n)-n=0
=>x^2+x(n-1)-n=0
Δ=(n-1)^2-4*(-n)
=n^2-2n+1+4n=(n+1)^2>=0
Để (P) tiếp xúc (d) thì n+1=0
=>n=-1
b: n=-1 nên (d): y=2x-1
(d1)//(d) nên (d1): y=2x+b
Thay x=2 vào y=x^2, ta được:
y=2^2=4
PTHĐGĐ là:
x^2-2x-b=0
Δ=(-2)^2-4*1*(-b)=4b+4
Để (d1) cắt (P) tại 2 điểm pb thì 4b+4>0
=>b>-1

Xét pt hoành độ gđ của (P) và (d) có:
\(x^2=mx+m+3\)
\(\Leftrightarrow x^2-mx-m-3=0\) (I)
Để (d) cắt (P) tại hai điểm pb ở bên phải trục tung
\(\Leftrightarrow\) Pt (I) có hai nghiệm dương
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta>0\\S>0\\P>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m^2+4m+12>0\left(lđ\right)\\m>0\\-m-3>0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\m< -3\end{matrix}\right.\)\(\Rightarrow m\in\varnothing\)
Vậy...

a:
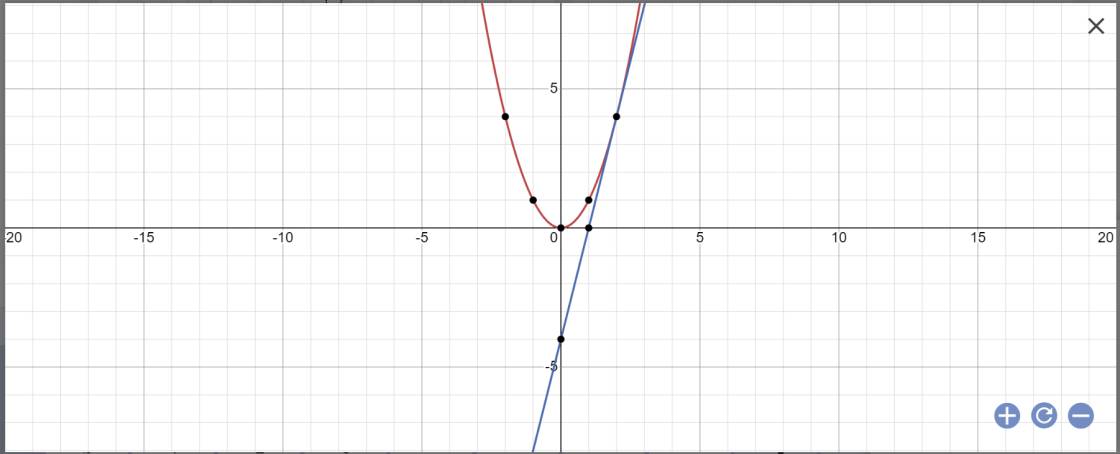
b: PTHĐGĐ là:
2x^2-(2m-2)x+m-1=0
Δ=(2m-2)^2-4*2*(m-1)
=4m^2-8m+4-8m+8
=4m^2-16m+12
=4m^2-2*2m*4+16-4=(2m-4)^2-4=(2m-6)(2m-2)
Để (d) cắt (P) tại 2 điểm pb thì (2m-6)(2m-2)>0
=>m>3 hoặc m<1

1: PTHĐGĐ là:
x^2-x-m+1=0(1)
Δ=(-1)^2-4(-m+1)=1+4m-4=4m-3
Để (P) cắt (d) tại hai điểm phân biệt thì 4m-3>0
=>m>3/4
Để (1) có hai nghiệm dương phân biệt thì m>3/4 và 1>0 và -m+1>0
=>m>3/4 và -m>-1
=>3/4<m<1

Phương trình hoành độ giao điểm là:
\(x^2-mx+2m-4=0\)
\(\Delta=\left(-m\right)^2-4\left(2m-4\right)\)
\(=m^2-8m+16=\left(m-4\right)^2\)
Để (P) cắt (d) tại hai điểm phân biệt thì m-4<>0
hay m<>4
Ta có: \(x_1^2+x_2^2\)
\(=\left(x_1+x_2\right)^2-2x_1x_2\)
\(=m^2-2\left(2m-4\right)\)
\(=m^2-4m+8\)
\(=\left(m-2\right)^2+4\ge4\forall x\)
Dấu '=' xảy ra khi m=2

a: y=mx+3
Thay x=1 và y=0 vào (d), ta được:
m+3=0
=>m=-3
b: PTHĐGĐ là:
x^2-mx-3=0
Vì a*c=-3<0
nên (P) luôn cắt (d) tại hai điểm phân biệt
|x1-x2|=2
=>\(\sqrt{\left(x_1-x_2\right)^2}=2\)
=>\(\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=2\)
=>\(\sqrt{m^2-4\left(-3\right)}=2\)
=>m^2+12=4
=>m^2=-8(loại)
=>KO có m thỏa mãn đề bài
Đường thẳng d: y = mx + n và parabol (P): y = a x 2 cắt nhau tại hai điểm phân biệt khi phương trình a x 2 = m . x + n có hai nghiệm phân biệt.
Đáp án: A