Giúp e câu b)c) ạ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
19 tháng 8 2023
a) \(A=\left(2\sqrt{12}-\sqrt{75}+\dfrac{1}{2}\sqrt{48}\right):\sqrt{3}\)
\(A=\left(4\sqrt{3}-5\sqrt{3}+2\sqrt{3}\right):\sqrt{3}\)
\(A=\sqrt{3}:\sqrt{3}\)
\(A=1\)
b) \(B=\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{\left(\sqrt{5}+1\right)^2}\)
\(B=\left|2-\sqrt{5}\right|-\left|\sqrt{5}+1\right|\)
\(B=-2+\sqrt{5}-\sqrt{5}-1\)
\(B=-3\)
c) \(C=\dfrac{3}{\sqrt{7}-2}-\dfrac{4}{3+\sqrt{7}}\)
\(C=\dfrac{3\left(\sqrt{7}+2\right)}{\left(\sqrt{7}-2\right)\left(\sqrt{7}+2\right)}-\dfrac{4\left(3-\sqrt{7}\right)}{\left(3+\sqrt{7}\right)\left(3-\sqrt{7}\right)}\)
\(C=\dfrac{3\left(\sqrt{7}+2\right)}{3}-\dfrac{4\left(3-\sqrt{7}\right)}{2}\)
\(C=\sqrt{7}+2-2\left(3-\sqrt{7}\right)\)
\(C=\sqrt{7}+2-6+2\sqrt{7}\)
\(C=3\sqrt{7}-4\)
d) \(D=3\sqrt{2a}-\sqrt{18a^3}+4\sqrt{\dfrac{a}{2}}-\dfrac{1}{4}\sqrt{128a}\)
\(D=3\sqrt{2a}-3a\sqrt{2a}+2\sqrt{2a}-\dfrac{1}{4}\cdot8\sqrt{2a}\)
\(D=5\sqrt{2a}-3a\sqrt{2a}-2\sqrt{2a}\)
\(D=3\sqrt{2a}-3a\sqrt{2a}\)
e) \(E=\dfrac{3+\sqrt{3}}{\sqrt{3}}-\dfrac{2}{\sqrt{3}-1}\)
\(E=\dfrac{\sqrt{3}\left(\sqrt{3}+1\right)}{\sqrt{3}}-\dfrac{2\left(\sqrt{3}+1\right)}{\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)}\)
\(E=\left(\sqrt{3}+1\right)-\dfrac{2\left(\sqrt{3}+1\right)}{2}\)
\(E=\left(\sqrt{3}+1\right)-\left(\sqrt{3}+1\right)\)
\(E=0\)
AH
Akai Haruma
Giáo viên
19 tháng 8 2023
Lời giải:
a.
\(A=2\sqrt{\frac{12}{3}}-\sqrt{\frac{75}{3}}+\frac{1}{2}\sqrt{\frac{48}{3}}=2\sqrt{4}-\sqrt{25}+\frac{1}{2}\sqrt{16}\)
\(2.2-5+\frac{1}{2}.4=1\)
b.
\(B=|2-\sqrt{5}|-|\sqrt{5}+1|=\sqrt{5}-2-(\sqrt{5}+1)=-3\)
c.
\(C=\frac{3(\sqrt{7}+2)}{(\sqrt{7}-2)(\sqrt{7}+2)}-\frac{4(3-\sqrt{7})}{(3+\sqrt{7})(3-\sqrt{7})}\)
\(=\frac{3(\sqrt{7}+2)}{7-2^2}-\frac{4(3-\sqrt{7})}{3^2-7}\)
\(=\frac{3(\sqrt{7}+2)}{3}-\frac{4(3-\sqrt{7})}{2}=\sqrt{7}+2-2(3-\sqrt{7})=-4+3\sqrt{7}\)
e.
\(E=\frac{\sqrt{3}(\sqrt{3}+1)}{\sqrt{3}}-\frac{2(\sqrt{3}+1)}{(\sqrt{3}-1)(\sqrt{3}+1)}=\sqrt{3}+1-\frac{2(\sqrt{3}+1)}{3-1^2}=(\sqrt{3}+1)-(\sqrt{3}+1)=0\)
17 tháng 6 2023
`@` `\text {Ans}`
`\downarrow`
`b,`
\(B=x^6 - 20x^5 - 20x^4 - 20x^3 - 20x^2 - 20x + 3\) tại `x=21`
Ta có: `20 = 21 - 1 => 20 = x-1`
Thay `20 = x-1` vào, ta có:
\(x^6-\left(x-1\right)x^5-\left(x-1\right)x^4-\left(x-1\right)x^3-\left(x-1\right)x^2-\left(x-1\right)x+3\)
`=`\(x^6-x^6+x^5-x^5+x^4-x^4+...+x+3\)
`=`\(x+3\)
`=`\(21+3=24\)
Vậy, `B=24`
17 tháng 6 2023
`c,`
`C=`\(x^7-26x^6+27x^5-47x^4-77x^3+50x^2+x-24\) tại `x=25`
`=`\(x^7-25x^6-x^6+25x^5+2x^5-50x^4+3x^4-75x^3-2x^3+50x^2+x-24\)
`=`\(x^6\left(x-25\right)-x^5\left(x-25\right)+2x^4\left(x-25\right)+3x^3\left(x-25\right)-2x^2\left(x-25\right)+x-24\)
`=`\(\left(x^6-x^5+2x^4+3x^3-2x^2\right)\left(x-25\right)+x-24\)
Thay `x=25` vào bt C, ta được:
\(\left(25^6-25^5+2\cdot25^4+3\cdot25^3-2\cdot25^2\right)\left(25-25\right)+25-24\)
`=`\(\left(25^6-25^5+2\cdot25^4+3\cdot25^3-2\cdot25^2\right)\cdot0+1\)
`= 0+1=1`
Vậy, `C=1.`
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
20 tháng 6 2023
\(a,\left(12x-5\right)\left(4x-1\right)+\left(3x-7\right)\left(1-16x\right)=81\\ \Leftrightarrow48x^2-20x-12x+5-3x-48x^2-7+112x-81=0\\ \Leftrightarrow77x=83\\ \Leftrightarrow x=\dfrac{83}{77}\)
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
20 tháng 6 2023
\(b,\left(x-4\right)\left(x-1\right)=\left(x-2\right)\left(x-3\right)\\ \Leftrightarrow x^2-4x-x+4=x^2-2x-3x+6\\ \Leftrightarrow x^2-x^2-4x-x+2x+3x=6-4\\ \Leftrightarrow0x=2\left(vô.lí\right)\)
Vậy không có x thoả mãn
K
2
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 3 2023
b.
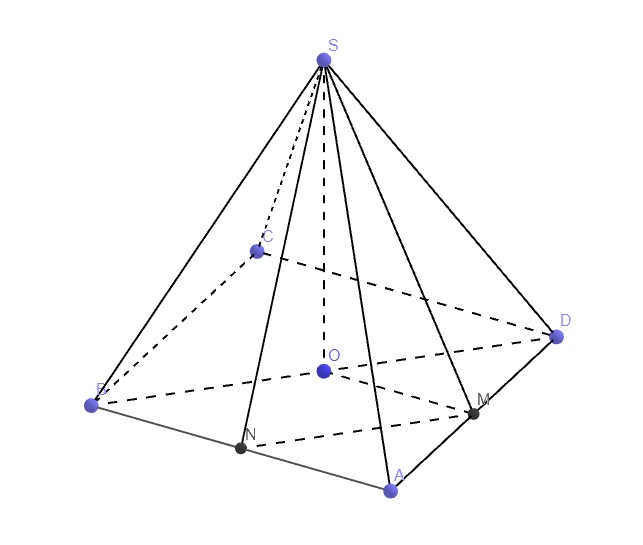
\(SO\perp\left(ABCD\right)\Rightarrow OM\) là hình chiếu vuông gốc của SM lên (ABCD)
\(\Rightarrow\widehat{SMO}\) là góc giữa SM và (ABCD)
\(BD=a\sqrt{2}\Rightarrow SO=\sqrt{SD^2-OD^2}=\sqrt{3a^2-\left(\dfrac{a\sqrt{2}}{2}\right)^2}=\dfrac{a\sqrt{10}}{2}\)
\(OM=\dfrac{1}{2}AB=\dfrac{a}{2}\)
\(\Rightarrow tan\widehat{SMO}=\sqrt{10}\Rightarrow\widehat{SMO}=...\)
b.
Gọi N là trung điểm AB \(\Rightarrow MN\) là đường trung bình tam giác ABD \(\Rightarrow\left\{{}\begin{matrix}MN=\dfrac{1}{2}BD=\dfrac{a\sqrt{2}}{2}\\MN||BD\end{matrix}\right.\)
\(\Rightarrow\widehat{\left(SM;BD\right)}=\widehat{\left(SM;MN\right)}=\widehat{SMN}\)
\(OM=ON\Rightarrow SN=SM=\sqrt{SO^2+OM^2}=\dfrac{a\sqrt{11}}{2}\)
Định lý hàm cos:
\(cos\widehat{SMN}=\dfrac{SM^2+MN^2-SN^2}{2SM.MN}=\dfrac{\sqrt{22}}{22}\Rightarrow\widehat{SMN}=...\)
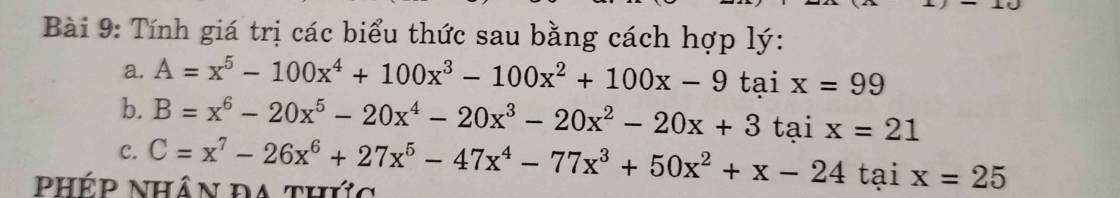
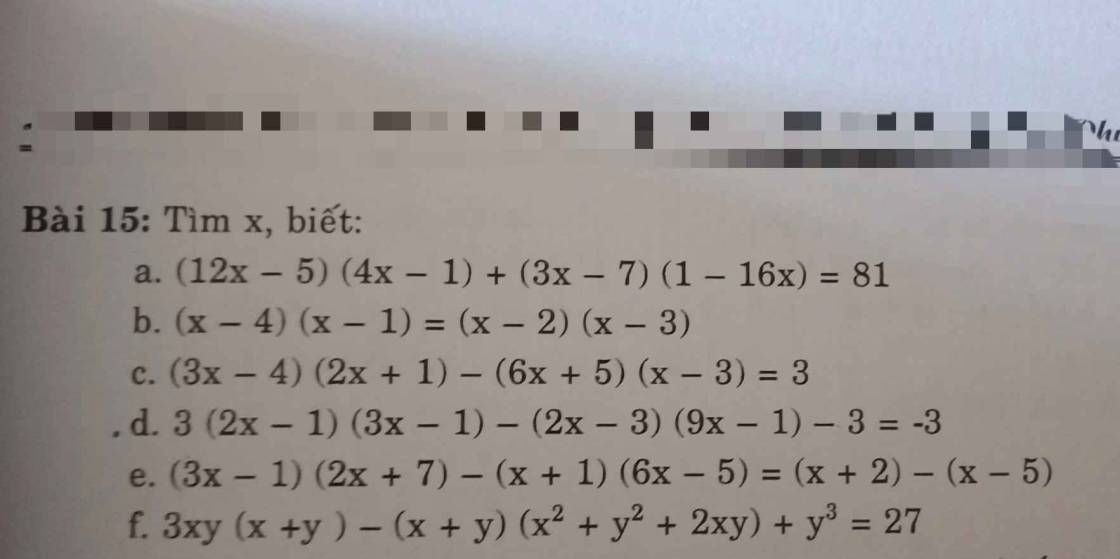
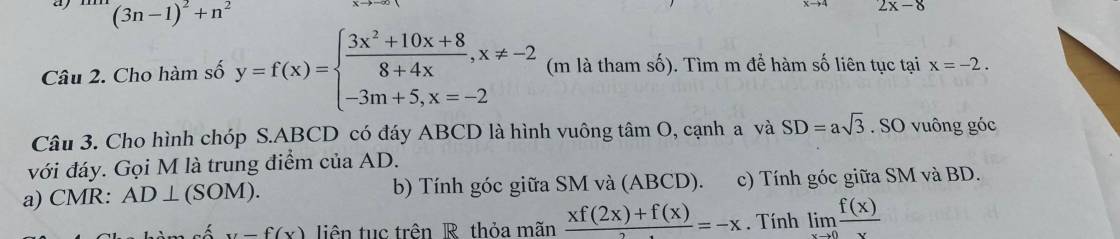
a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình củaΔABC
Suy ra: MN//BC
hay MNCB là hình thang