Giải giúp mình với gấp lắm rồi.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


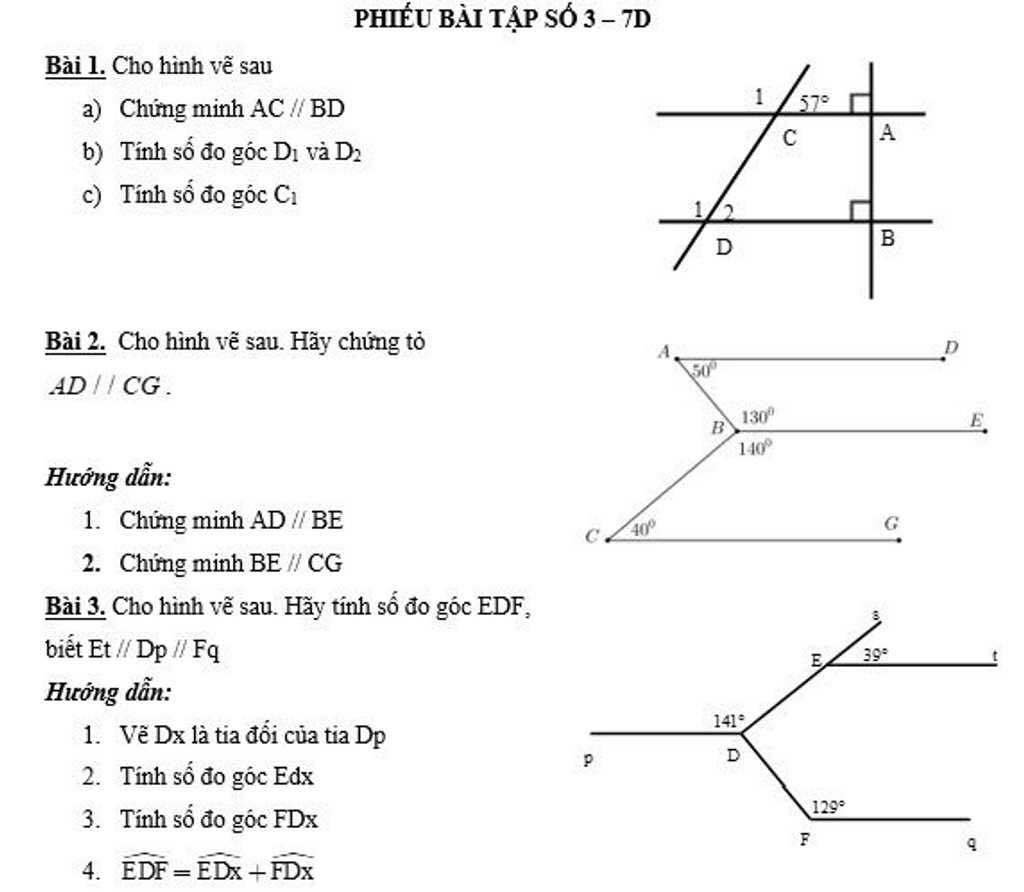
\(1,\\ a,\left\{{}\begin{matrix}AC\perp AB\\BD\perp AB\end{matrix}\right.\Rightarrow AC//BD\\ b,AC//BD\Rightarrow\widehat{D_2}=\widehat{C_1}=57^0\left(đồng.vị\right)\\ \widehat{D_2}+\widehat{D_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{D_1}=180^0-57^0=123^0\\ c,AC//BD\Rightarrow\widehat{D_1}=\widehat{C_1}=123^0\left(đồng.vị\right)\)
\(2,\\ \widehat{DAB}+\widehat{ABE}=50^0+130^0=180^0\)
Mà 2 góc này ở vị trí TCP nên AD//BE (1)
\(\widehat{EBC}+\widehat{BCG}=140^0+40^0=180^0\)
Mà 2 góc này ở vị trí TCP nên BE//CG (2)
Từ (1)(2) ta được AD//CG

#include <bits/stdc++.h>
using namespace std;
double a,b;
int main()
{
cin>>a>>b;
cout<<(a+b)*2;
return 0;
}

a, 7+4+1=12 => Để số chia hết cho 9 thì * = 18 - 12= 6
b, 5+2+2=9 => Để số chia hết cho 3 thì *=3 hoặc *=6 hoặc *=9 hoặc *=0
c, * ở hàng đơn vị chia hết cho 2 và 5 => * hàng đơn vị: 0
1+8+2+0 =11. Để số chia hết cho 3 và 9 => * ở hàng nghìn là: 18 - 11 = 7

Áp dụng định lí Pytago vào ΔABD vuông tại A, ta được:
\(AB^2+AD^2=BD^2\)
\(\Leftrightarrow BD^2=6^2+8^2=100\)
hay BD=10(cm)
Ta có: ABCD là hình chữ nhật
mà O là giao điểm của hai đường chéo AC và BD
nên O là trung điểm chung của AC và BD
Áp dụng hệ thức lượng trong tam giác vuông vào ΔBAD vuông tại A có AH là đường cao ứng với cạnh huyền BD, ta được:
\(AH\cdot BD=AB\cdot AD\)
\(\Leftrightarrow AH=4.8\left(cm\right)\)
Ta có: ΔABD vuông tại A
mà AO là đường trung tuyến ứng với cạnh huyền BD
nên \(AO=\dfrac{BD}{2}=\dfrac{10}{2}=5\left(cm\right)\)
Áp dụng định lí Pytago vào ΔAHO vuông tại H, ta được:
\(AO^2=AH^2+HO^2\)
\(\Leftrightarrow HO^2=5^2-4.8^2=1.96\)
hay HO=1,4(cm)
Diện tích tam giác AHO là:
\(S_{AHO}=\dfrac{HA\cdot HO}{2}=\dfrac{1.4\cdot4.8}{2}=3.36\left(cm^2\right)\)

a, \(2y^2\left(8y^6\right)y=16y^9\)
b, \(=\dfrac{3}{4}x^3y^4\)
c, \(=10x^3y^4z^8\)
d, \(=\left(\dfrac{3}{4}x^2y^3\right)\left(\dfrac{12}{5}x^4\right)=\dfrac{9}{5}x^6y^3\)
e, \(=-\dfrac{5}{4}x^5y^{10}\)
f, \(=120x^4y^6z^4\)


a: Xét ΔABH vuông tại H và ΔMBH vuông tại H có
HB chung
HA=HM
Do đó: ΔABH=ΔMBH

\(a,\Rightarrow20\cdot2^x=160+1-1\\ \Rightarrow2^x=160:20=8=2^3\\ \Rightarrow x=3\\ b,\Rightarrow\left(4-x:2\right)^3=2\left(8-5\right)+1+1\\ \Rightarrow\left(4-x:2\right)^3=6+2=8=2^3\\ \Rightarrow4-x:2=2\\ \Rightarrow x:2=2\Rightarrow x=4\\ c,n\left(n+2017\right)\)
Với n chẵn thì \(n=2k\left(k\in N\right)\Rightarrow n\left(n+2017\right)=2k\left(n+2017\right)⋮2\)
Với n lẻ thì \(n=2k+1\left(k\in N\right)\Rightarrow n\left(n+2017\right)=n\left(2k+2018\right)=2n\left(k+1009\right)⋮2\)
Vậy \(n\left(n+2017\right)\) luôn chẵn
\(d,3^{200}=\left(3^2\right)^{100}=9^{100}>8^{100}=\left(2^3\right)^{100}=2^{300}\)
 Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi
Mn giải giúp mình với mình cần gấp lắm hôm nay mình pgair nộp rồi








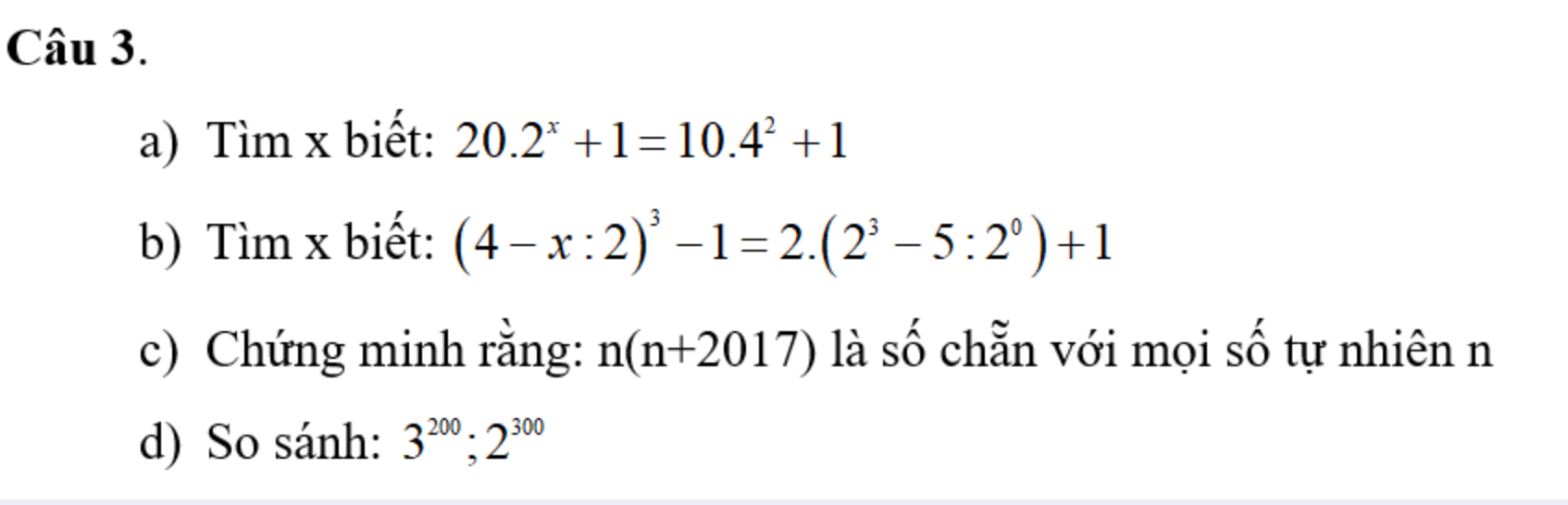 giúp mình với, mình cần gấp lắm, 5p phải nộp rồi
giúp mình với, mình cần gấp lắm, 5p phải nộp rồi