Hình chóp S.ABC có đáy ABC là tam giác vuông cân ( BA = BC ), cạnh bên SA vuông góc với mặt phẳng đáy và có độ dài là a 3 , cạnh bên SB tạo với đáy một góc 60 o . Tính diện tích toàn phần của hình chóp
A. 3 + 3 + 6 2 a 2
B. 3 + 6 2 a 2
C. 3 + 6 2 a 2
D. 3 - 6 2 a 2

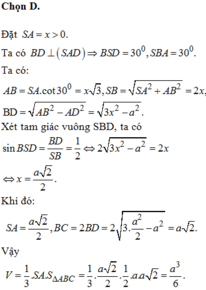
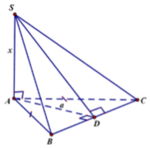
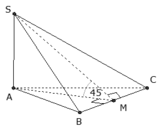
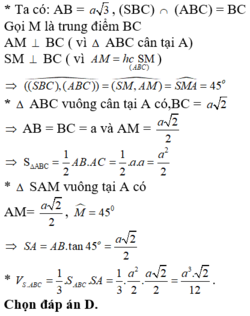
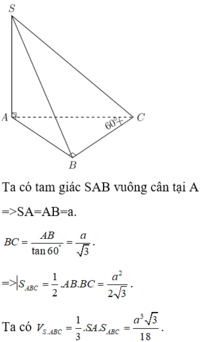

Ta có: S A ⊥ A B ; S A ⊥ A C ; B C ⊥ A B ; B C ⊥ S A
Suy ra, B C ⊥ S A B nên: B C ⊥ S B
Do đó, tứ diện S.ABC có 4 mặt đều là các tam giác vuông.
Ta có: AB là hình chiếu của SB lên (ABC) nên S B A ^ = 60 o
tan S B A ^ = S A A B ⇒ A B = S A tan S B O ^ = a 3 3 = a = B C A C = A B 2 + B C 2 = a 2 + a 2 = a 2 S B = S A 2 + A B 2 = a 3 3 + a 2 = 2 a
Do đó ta có
S t p = S S A B + S S B C + S S A C + S A B C = 1 2 S A . A B + S B . B C + S A . A C + A B . B C = 1 2 a 3 . a + 2 a . a + a 3 . a 2 + a . a = 3 + 3 + 6 2 a 2
Vậy S t p = 3 + 3 + 6 2 a 2
Đáp án A