Người ta trồng cây theo hình tam giác, với quy luật: ở hàng thứ nhất có 1 cây, ở hàng thứ hai có 2 cây, ỏ hàng thứ 3 có 3 cây,… ở hàng thứ n có n cây. Biết rằng người ta trồng hết 4950 cây. Hỏi số hàng cây được trồng theo cách trên là nbao nhiêu?
A. 101
B. 100
C. 99
D. 98


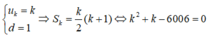
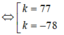
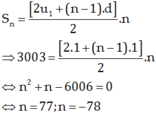
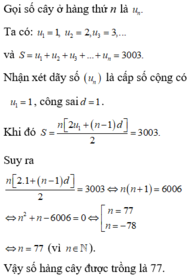

Đáp án C.
Phương pháp: Sử dụng tổng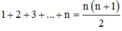
Cách giải: Giả sử trồng được n hàng cây với quy luật trên thì số cây trồng được là: