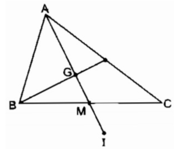
Cho tam giác ABC, gọi M là trung điểm của BC, G là trọng tâm của tam giác ABC, lấy D đối xứng với A qua M, I là trọng tâm của tam giác ABC.
a) Chứng minh rằng \(\overrightarrow{IG}=\frac{1}{3}\overrightarrow{AB}+\overrightarrow{DM}\)
b) Lấy J thỏa mãn \(2\overrightarrow{CJ}=2\overrightarrow{AB}+\overrightarrow{JM}\) Chứng minh rằng IJ song song với AB
c) Giả sử AB= a, BC=2a và \(\widehat{ABC}=60^o\) Tính độ dài của \(\overrightarrow{u}=\overrightarrow{AB}+2\overrightarrow{AC}\)
d) Xác định tập hợp điểm E thỏa mãn \(\left|2\overrightarrow{EA}-3\overrightarrow{EB}+5\overrightarrow{EC}\right|=2\left|\overrightarrow{ED}+\overrightarrow{EG}\right|\)