K
Khách
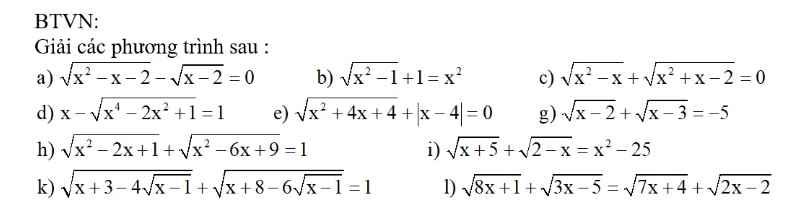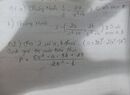
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
X
0
Những câu hỏi liên quan
93
1
MR
0
MR
1
NL
3
20 tháng 10 2021
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\le-1\\x\ge2\end{matrix}\right.\)
\(\sqrt{x^2-x-2}-\sqrt{x-2}=0\\ \Leftrightarrow\sqrt{x^2-x-2}=\sqrt{x-2}\\ \Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow x\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x=2\left(tm\right)\end{matrix}\right.\)
20 tháng 10 2021
\(a,ĐK:x\ge2\\ PT\Leftrightarrow x^2-x-2=x-2\\ \Leftrightarrow x^2-2x=0\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(tm\right)\\x=0\left(ktm\right)\end{matrix}\right.\Leftrightarrow x=2\\ b,ĐK:\left[{}\begin{matrix}x\le-1\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-1}=x^2-1\\ \Leftrightarrow x^2-1=\left(x^2-1\right)^2\\ \Leftrightarrow\left(x^2-1\right)\left(x^2-1-1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x-\sqrt{2}\right)\left(x+\sqrt{2}\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=1\left(tm\right)\\x=-1\left(tm\right)\\x=\sqrt{2}\left(tm\right)\\x=-\sqrt{2}\left(tm\right)\end{matrix}\right.\)
\(c,ĐK:\left[{}\begin{matrix}x\le-2\\x\ge1\end{matrix}\right.\\ PT\Leftrightarrow\sqrt{x^2-x}=-\sqrt{x^2+x-2}\\ \Leftrightarrow x^2-x=x^2+x-2\\ \Leftrightarrow2x=2\\ \Leftrightarrow x=1\left(tm\right)\)
VD
29 tháng 5 2022
Hướng dẫn: A đạt GTLN khi \(\dfrac{1}{A}\) đạt GTNN
Ta có: \(x^2+2\ge0\forall x\)
\(\Rightarrow A=\dfrac{1}{x^2+2}\le\dfrac{1}{2}\forall x\)
Vậy GTLN của A là 1/2
=> A
10 tháng 12 2021
\(a,a^2-10a+25=\left(a-5\right)^2\\ b,4x^2+4x+1=\left(2x+1\right)^2\\ c,4x^2-9=\left(2x-3\right)\left(2x+3\right)\\ d,x^3+3x^2+3x+1=\left(x+1\right)^3\\ e,a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3\\ f,y^3+8=\left(y+2\right)\left(y^2-2y+4\right)\\ g,27x^3-1=\left(3x-1\right)\left(9x^2+3x+1\right)\)
10 tháng 12 2021
\(a^2-10x+25=\left(a-5\right)^2\)
b/ \(4x^2+4x+1=\left(2x+1\right)^2\)
c/ \(4b^2-9=\left(2b-3\right)\left(2b+3\right)\)
d/ \(x^3+3x^2+3x+1=\left(x+1\right)^3\)
e/ \(a^3-3a^2b+3ab^2-b^3=\left(a-b\right)^3\)
f/ \(y^3+8=\left(y+2\right)\left(y^2-2y+4\right)\)
g/ \(27x^3-1=\left(3x-1\right)\left(9x^2+3x+1\right)\)
V
0
93
1
11 tháng 11 2021
a: Xét (O) có
EM là tiếp tuyến
EN là tiếp tuyến
Do đó: EM=EN
hay E nằm trên đường trung trực của MN(1)
Ta có: OM=ON
nên O nằm trên đường trung trực của MN(2)
Từ (1) và (2) suy ra OE là đường trung trực của MN