K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 3 2022
Chắc là biến đổi trong bài tìm pt mặt phẳng
Từ hệ 2 pt đầu ta rút ra được: \(\left\{{}\begin{matrix}c=-a-b\\d=2a+b\end{matrix}\right.\)
Thế vào pt cuối:
\(\dfrac{\left|3a-b\right|}{\sqrt{a^2+b^2+\left(a+b\right)^2}}=\dfrac{3}{\sqrt{2}}\)
\(\Rightarrow2\left(3a-b\right)^2=9\left(a^2+b^2\right)+9\left(a+b\right)^2\)
\(\Rightarrow15ab+8b^2=0\Rightarrow\left[{}\begin{matrix}b=0\\b=-\dfrac{15a}{8}\end{matrix}\right.\)
TL
2
16 tháng 11 2021
Câu 1.
Tờ vé số có dạng \(\overline{a_1a_2a_3a_4a_5a_6}\in A=\left\{0;1;2;3;4;5;6;7;8;9\right\}\)
\(;a_i\ne a_j\)
Chọn \(a_1\ne0\) nên \(a_1\) có 9 cách chọn.
5 số còn lại là chỉnh hợp chập 5 của 8 số còn lại \(\in A\backslash\left\{a_1\right\}\)
\(\Rightarrow\)Có \(A_8^5\) cách.
Vậy có tất cả \(A_8^5\cdot9=60480\) vé số.
10 tháng 7 2021
\(A=\left(t+2\right)\left(3t-1\right)-t\left(3t+3\right)-2t+7\)
\(=3t^2-t+6t-2-3t^2-3t-2t+7\)
\(=\left(3t^2-3t^2\right)-\left(t-6t+3t+2t\right)-\left(2-7\right)\)
\(=0-0-\left(-5\right)=5\)
HV
10 tháng 7 2021
A=(t+2)(3t−1)−t(3t+3)−2t+7A=(t+2)(3t−1)−t(3t+3)−2t+7
=3t2−t+6t−2−3t2−3t−2t+7=3t2−t+6t−2−3t2−3t−2t+7
=(3t2−3t2)−(t−6t+3t+2t)−(2−7)=(3t2−3t2)−(t−6t+3t+2t)−(2−7)
=0−0−(−5)=5
NT
0
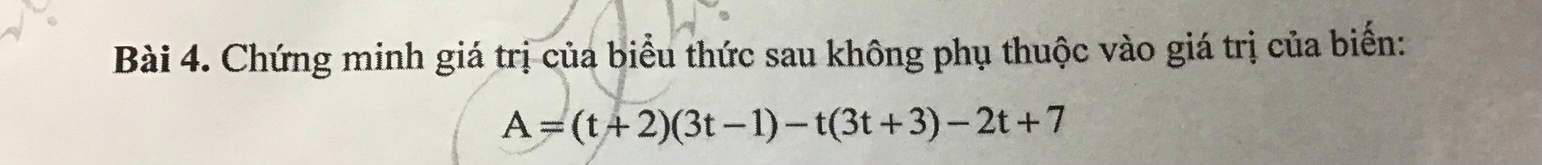
a, Ta có: M là trung điểm của AB
N là trung điểm của AC
mà AB = AC
=> AM = AN
Xét \(\Delta AHM\)và\(\Delta AHN\)ta có:
AM = AN (gt)
MH = NH (H là trung điểm của MN)
AH cạnh chung
=> \(\Delta AHM=\Delta AHN\left(c.c.c\right)\)
Vậy \(\Delta AHM=\Delta AHN\left(ĐPCM\right)\)
b,Ta có: \(\Delta AHM=\Delta AHN\)(câu a)
=> \(\widehat{MAH}=\widehat{NAH}\)(2 góc tương ứng)
=> AH là tia phân giác của góc A
Vậy AH là tia phân giác của góc A (ĐPCM)
c, Xét \(\Delta ABK\)và \(\Delta ACK\)ta có:
AB = AC (gt)
BK = CK (K là trung điểm của BC)
AK cạnh chung
=> \(\Delta ABK=\Delta ACK\left(c.c.c\right)\)
=> \(\widehat{BAK}=\widehat{CAK}\)(2 góc tương ứng)
=> AK là tia phân giác của góc A
mà AH là tia phân giác của góc A
=> 3 điểm A, H, K thẳng hàng