Biết rằng hai giá trị x1 , x2 của x có tổng bằng -2 thì hai giá trị tương ứng y1 , y2 của y có tổng bằng 6. Hỏi hai đại lượng x và y liên hệ với nhau bởi công thức nào?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 1
a: x và y tỉ lệ thuận nên \(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x_1}{y_1}=\dfrac{x_2}{y_2}=\dfrac{x_1+x_2}{y_1+y_2}=\dfrac{6}{-2}=-3\)
=>x=-3y
b: x=-3y
=>\(y=-\dfrac{1}{3}x\)
Thay x=2 vào \(y=-\dfrac{1}{3}x\), ta được:
\(y=-\dfrac{1}{3}\cdot2=-\dfrac{2}{3}\)
Thay x=4 vào \(y=-\dfrac{1}{3}x\), ta được:
\(y=-\dfrac{1}{3}\cdot4=-\dfrac{4}{3}\)
14 tháng 11 2021
cho x và y là hai đại lượng tỉ lệ thuận, biết rằng hai giá trị bất kì x1,x2 của x có tổng bằng 1, hai giá trị tương ứng y1,y2 của y có tổng bằng 5
a, hãy biểu diễn y theo x
b, tính giá trị của x khi y=-4 , y= -1 và 1 phần 2
c, giá trị của y khi x=-4, x=0,5
ht
14 tháng 11 2021
cho x và y là hai đại lượng tỉ lệ thuận, biết rằng hai giá trị bất kì x1,x2 của x có tổng bằng 1, hai giá trị tương ứng y1,y2 của y có tổng bằng 5
a, hãy biểu diễn y theo x
b, tính giá trị của x khi y=-4 , y= -1 và 1 phần 2
5 tháng 12 2015
Theo de ta co:
y1/x1 = y2/x2
=> y1/x1 = y2/x2 = (y1+y2) / (x1+x2) = (-10/3)/(5/3) = -2
=> y1=-2.x1 ; y2=-2.x2
Váy: x liên hệ với y theo công thức y=-2.x hay x = -1/2.ý
BH
20 tháng 8 2017
a)Vì x và y là hai đại lượng tỉ lệ thuận nên:
y = a.x
=> a = y/x
Do đó: y1/x1 = y2/x2 = y1+y2/x1x2 = 3k^2/4k = 3k/4
=> 3k/4 = y/x
=> y = 3k/4.x
b)Với k = 4 ta có:
y = 3k/4.x
=> y = 3.4/4.x
=> y = 3.x
=> 3 = y/x
Do đó: y1/x1 = 3
=> y1 = x1.3
Và y1+x1 = 5
=> x1.3+x1 = 5
=> 4.x1 = 5
=> x1 = 5/4
Vì x1 = 5/4
=> y1 = 5/4.3 = 15/4
Vậy: y1 = 15/4
x1 = 5/4
CM
1 tháng 9 2017
Vì x và y là hai đại lượng tỉ lệ thuận nên theo tính chất của đại lượng tỉ lệ thuận ta có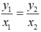 
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
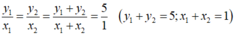
Vậy y và x tỉ lệ thuận với nhau theo hệ số tỉ lệ là 5
Suy ra y = 5x
Chọn đáp án B.
\(x\)và \(y\)là hai đại lượng tỉ lệ thuận với nhau nên đặt \(y=ax\)\(\left(a\ne0\right)\).
Theo đề ta có: \(\hept{\begin{cases}x_1+x_2=-2\\y_1+y_2=6\end{cases}\Rightarrow\hept{\begin{cases}x_1+x_2=-2\\ax_1+ax_2=6\end{cases}\Leftrightarrow}\hept{\begin{cases}x_1+x_2=-2\\a\left(x_1+x_2\right)=6\end{cases}}\Rightarrow a=-3}\).
Vậy \(y=-3x\).