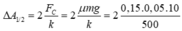Dùng lò xo có độ cứng 100N/m để kéo một khối gỗ nặng 20N chuyển động thẳng đều trên mặt bàn, gỗ nằm ngang. Lò xo nằm ngang, tính độ dãn của lò xom biết hệ ma sát giữa khối gỗ với mặt bàn là 0,3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án B
+ Xét trong nửa chu kì đầu tiên thì biên độ của con lắc giảm 1 lượng là:
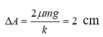
+ Vì kéo khúc gỗ ra vị trí dãn 40 cm nên biên độ ban đầu là 8 cm.
+ Sau nửa chu kì đầu tiên thì chiều dài của con lắc chính là chiều dại ngắn nhất mà lò xo đạt được khi dao động là
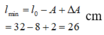

Hướng dẫn:
Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 2.40.10 − 3 .10 20 = 4 m m
→ Biên độ dao động của lò xo trong nửa chu kì đầu A 1 = X 0 – x 0 = 6 – 0 , 4 = 5 , 6 c m .
+ Lò xo bị nén lớn nhất khi vật đi đến biên âm ứng với nửa chu kì đầu.
→ Độ nén của lò xo khi đó là Δ l m a x = A 1 + x 0 = 5 , 6 – 0 , 4 = 5 , 2 c m .
Đáp án A

Chọn C

+ Độ giảm biên độ trong nửa chu kì: ![]()
+ Theo yêu cầu của đề: 0,04 + (0,04 – ΔA) < S < 0,04 + 2(0,04 – ΔA)
=> 0,08 – 0,4μ < S < 0,12 – 0,8μ
+ Tới khi dừng hẳn: ![]()
+ 0,08 – 0,4μ < 4.10-3 /μ => (μ – 0,1)2 > 0
+ 4.10-3 /μ < 0,12 – 0,8μ => μ2 – 0,15μ + 0,005 < 0 => 0,05 < μ < 0,1.

a/ \(W=\dfrac{1}{2}kx^2+\dfrac{1}{2}mv^2=\dfrac{1}{2}k\Delta l^2\)
\(\Leftrightarrow kx^2+mv^2=k\Delta l^2\Leftrightarrow v=\sqrt{\dfrac{k\Delta l^2-kx^2}{m}}=\sqrt{\dfrac{40.0,02^2-40x^2}{0,4}}\left(m/s\right)\)
b/ \(v_{max}\Leftrightarrow\dfrac{40.0,02^2-40x^2}{0,4}\left(max\right)\Leftrightarrow x=0\) => khi nó ở VTCB
\(\Rightarrow v_{max}=\dfrac{40.0,02^2}{0,4}\left(m/s\right)\)

Hướng dẫn: Chọn đáp án C
Cách 1: Độ giảm cơ năng đúng bằng công của lực ma sát:

![]()
Cách 2: Xem I là tâm dao động và biên độ A 1 = A - x 1 , tốc độ tại O:
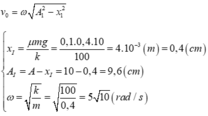
![]()