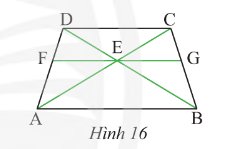
CHo hình thang cân ABCD đáy lớn CD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BD, CD, CA. Chứng minh rằng EG là tia phân giác của góc FEH
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔABC có
E là trung điểm của AB
H là trung điểm của AC
Do đó: EH là đường trung bình của ΔABC
Suy ra: EH//BC và EH=BC/2(1)
Xét ΔBDC có
F là trung điểm của BD
G là trung điểm của CD
Do đó: FG là đường trung bình của ΔBDC
Suy ra: FG//BC và FG=BC/2(2)
Xét ΔABD có
E là trung điểm của AB
F là trung điểm của BD
Do đó: EF là đường trung bình của ΔABD
Suy ra: EF//AD và EF=AD/2
hay EF=BC/2(3)
Từ (1) và (2) suy ra EH//FG và EH=FG
Từ (2) và (3) suy ra EF=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
Do đó: EHGF là hình bình hành
mà EF=FG
nên EHGF là hình thoi

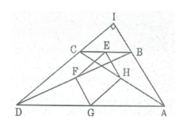
* Trong ∆ BCD, ta có:
E là trung điểm của BC (gt)
F là trung điểm của BD (gt)
Suy ra EF là đường trung bình của ∆ BCD
⇒ EF // CD và EF = 1/2 CD (1)
* Trong ∆ ACD, ta có: H là trung điểm của AC (gt)
G là trung điểm của AD (gt)
Suy ra HG là đường trung bình của ∆ ACD
⇒HG // CD và HG = 1/2 CD (2)
Từ (1) và (2) suy ra: EF // HG và EF = HG
Suy ra tứ giác EFGH là hình bình hành (vì có một cặp cạnh đối song song và bằng nhau).
* Mặt khác: EF // CD (chứng minh trên)
AB ⊥ CD (gt)
Suy ra EF ⊥ AB
Trong ∆ ABC ta có HE là đường trung bình ⇒ HE // AB
Suy ra: HE ⊥ EF hay ∠ (FEH) = 90 0
Vậy hình bình hành EFGH là hình chữ nhật.

ΔDFG= ΔCHG(GD=GC;DF=CH;góc FDG=gócHCG)
=>GF=GH(1)
ΔEFB= ΔEHA(FB=HA;EB=EA;gócEAH=gócABF)
=>EF=EH(2)
TỪ 1 và 2=> tứ giác EFGH là hình thoi

+ Xét tg BCD có EF là đường trung bình => EF//=CD/2
+ Xét tg ACD có GH là đường trung bình => GH//=CD/2
=> EF//=GH => EFGH là hình bình hành (1)
+ Xét tg ABC có HE là đường trung bình => HE=AB/2 mà EF=CD/2 và AB=CD => EF=HE (2)
Từ 91) và (2) => EFGH là hình thoi => EG vuông góc với FH (2 đường chéo của hình thoi vuông góc với nhau)

Vì \(EG\) // \(AB\) (gt)
suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{CAB}}}\) (đồng vị) và \(\widehat {{\rm{GEB}}} = \widehat {{\rm{EBA}}}\) (1)
Xét \(\Delta CAB\) và \(\Delta DBA\) ta có:
\(AC = BD\) (tính chất hình thang cân)
\(BC = AD\) (tính chất hình thang cân)
\(AB\) chung
Suy ra \(\Delta CAB = \Delta DBA\) (c-c-c)
Suy ra \(\widehat {{\rm{CAB}}} = \widehat {{\rm{EAB}}}\) (2)
Từ (1) và (2) suy ra \(\widehat {{\rm{CEG}}} = \widehat {{\rm{GEB}}}\)
Suy ra \(EG\) là phân giác của \(\widehat {{\rm{CEB}}}\)