cho hình bình hành ABCD.Lấy điểm H trên cạnh AB và điểm K trên tia đối của tia CB sao cho tam giác KAB cân tại A,tam giác HBC cân tại C.Chứng minh rằng tam giác KDH là tam giác cân
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



ΔABC cân tại A suy ra 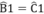
Ta lại có :
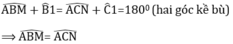
- ΔABM và ΔACN có
AB = AC (Do ΔABC cân tại A).
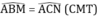
BM = CN(gt)
⇒ ΔABM = ΔACN (c.g.c)
⇒ AM = AN (hai cạnh tương ứng) ⇒ ΔAMN cân tại A.

Bạn tự vẽ hình nhé ^^
1. ta có AC=CM ; BC=CE => tứ giác ABME là hình bình hành ( hai đường chéo cắt nhau tại trung điểm của mỗi đường)
2. Ta có ME=AB
mà AB=AC=CM => CM=ME (=AB)
=> tam giác MEC cân tại M
3. Xét tam giác AMN có
(1) AB=BN ; AC=CM => BC // MN (đường thẳng đi qua trung điểm của hai cạnh trong một tam giác sẽ song song với cạnh còn lại. Đường TB của tam giác) => BCMN là hình thang
(2) Ta có BN=CM (g.thiết)
từ (1) và (2) => tứ giác BCMN là hình thang cân (vì có hai cạnh bên là BN và CM bằng nhau)
4. Xét tam giác BCM và BNC có
CB: chung
BM=CN (hai đg chéo hình thang cân)
BN=CM (giả thiết)
=> tam giác BCM=BNC
=> Góc MBC=góc BCN
mà góc FCE =gócBCN (đối đỉnh)
gócMBC= FEC (so le trong)
=.> góc FEC= FCE
=>tam giác EFC cân tại F
=> FE=FC (1)
theo CM ý b) ta có ME=MC (2)
từ 1 và 2 suy ra FM là đường trung trực của EC => FM vuông góc với EC => FM vuông goc với MN tại M
Mà MN//EC
=> tam giác MNF vuông tại M

a: Ta có: AE+BE=AB
AF+FC=AC
mà AB=AC
và BE=FC
nên AE=AF
hay ΔAEF cân tại A
b: Xét ΔABC có AE/AB=AF/AC
nên EF//BC
=>\(\widehat{AEF}=\widehat{ABC}=\widehat{ACB}\)

Từ đỉnh A kẻ đường cao AH (H thuộc BC) (1)
Ta có : tam giác ABC cân tại A (gt) (2)
Từ(1) và(2)=> HB=HC(=1/2 BC) (3)
Lại có: BM=CN (gt) (4)
M nằm trên tia đối của tia BC, N nằm trên tia đối của tia CB => M,B,C.N thẳng hàng (5)
Từ (3)và (4)=>HB+BM=HC+CN (6)
Từ (5) và (6)=>AH vừa là đường cao, vừa là đường trung tuyến trong tam giác AMN
=> Tam giác AMN cân tại A (đpcm)

Hình vẽ:
Giải:
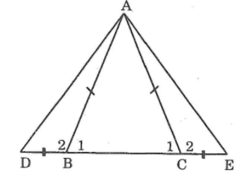
Vì tam giác \(ABC\) cân tại \(A\):
\(\Rightarrow\widehat{ABC}=\widehat{ACB}\)
\(\Rightarrow\widehat{ABD}=\widehat{ACE}\) ( góc bù )
Xét \(\Delta ABD\) và \(\Delta ACE\) có:
\(AB=AC \) \(\left(gt\right)\)
\(\widehat{ABD}=\widehat{ACE}\) \(\left(cmt\right)\)
\(BD=CE \) \(\left(gt\right)\)
Do đó: \(\Delta ABD=\Delta ACE\) \(\left(c.g.c\right)\)
\(\Rightarrow AD=AE\) ( cặp cạnh tương ứng )
\(\Rightarrow\Delta ADE\) cân tại \(A\).
Bài làm
Bạn tự vẽ hình nhé
Vì tam giác ABCABC cân tại A:
⇒ˆABC=ˆACB⇒ABC^=ACB^
⇒ˆABD=ˆACE⇒ABD^=ACE^ ( góc bù )
Xét ΔABDΔABD và ΔACEΔACE có:
AB=ACAB=AC (gt)
ˆABD=ˆACEABD^=ACE^ (cmt)
BD=CEBD=CE (gt)(gt)
Do đó: ΔABD=ΔACEΔABD=ΔACE (c.g.c)(c.g.c)
⇒AD=AE⇒AD=AE ( cặp cạnh tương ứng )
⇒ΔADE⇒ΔADE cân tại A

a: Xét ΔABD và ΔACE có
AB=AC
\(\widehat{ABD}=\widehat{ACE}\)
BD=CE
DO đó: ΔABD=ΔACE
Suy ra: AD=AE
hay ΔADE cân tại A
b: Xét ΔABH vuông tại H và ΔACK vuông tại K có
AB=AC
\(\widehat{HAB}=\widehat{KAC}\)
Do đó: ΔABH=ΔACK
Suy ra: BH=CK và AH=AK
Xét ΔADE có
AH/AD=AK/AE
nên HK//DE
hay HK//BC
c: Xét ΔHBD vuông tại H và ΔKCE vuông tại K có
BD=CE
\(\widehat{HBD}=\widehat{KCE}\)
Do đó: ΔHBD=ΔKCE
Suy ra: \(\widehat{HBD}=\widehat{KCE}\)
=>\(\widehat{OCB}=\widehat{OBC}\)
=>ΔOBC cân tại O
=>OB=OC
mà HB=CK
nên OB+HB=OC+CK
=>OH=OK
hay ΔOHK cân tại O

*) Ta có: ΔABC cân tại A

BD = CE (giả thiết)
Suy ra: ΔABD = ΔACE (c.g.c)
⇒ AD = AE ( hai cạnh tương ứng)
*) Tam giác ADE có AD = AE nên tam giác này cân tại A (theo định nghĩa tam giác cân)

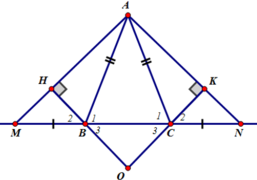
a) Ta có: \(\widehat{ABM}+\widehat{ABC}=180^0\)(hai góc kề bù)
\(\widehat{ACN}+\widehat{ACB}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
BM=CN(gt)
Do đó: ΔABM=ΔACN(c-g-c)
Suy ra: AM=AN(hai cạnh tương ứng)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
b) Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
BM=CN(gt)
\(\widehat{HMB}=\widehat{KNC}\)(hai góc ở đáy trong ΔAMN cân tại A)
Do đó: ΔHBM=ΔKCN(cạnh huyền-góc nhọn)
Suy ra: BH=CK(hai cạnh tương ứng)
c) Ta có: ΔHBM=ΔKCN(cmt)
nên HM=KN(hai cạnh tương ứng)
Ta có: AH+HM=AM(H nằm giữa A và M)
AK+KN=AN(K nằm giữa A và N)
mà AM=AN(cmt)
và HM=KN(cmt)
nên AH=AK(đpcm)
d) Ta có: ΔHBM=ΔKCN(cmt)
nên \(\widehat{HBM}=\widehat{KCN}\)(hai góc tương ứng)
mà \(\widehat{OBC}=\widehat{HBM}\)(hai góc đối đỉnh)
và \(\widehat{OCB}=\widehat{KCN}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định lí đảo của tam giác cân)

a: Xét ΔABD và ΔACE có
AB=AC
góc ABD=góc ACE
BD=CE
=>ΔABD=ΔACE
=>AD=AE
b:
Xét ΔBHD vuông tại H và ΔCKE vuông tại K có
BD=CE
góc D=góc E
=>ΔBHD=ΔCKE
=>góc HBD=góc KCE
=>góc IBC=góc ICB
=>ΔIBC cân tại I
c: Xét ΔABI và ΔACI có
AI chung
AB=AC
BI=CI
=>ΔABI=ΔACI
=>góc BIA=góc CIA
=>IA là phân giác của góc BIC