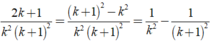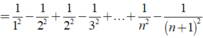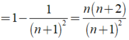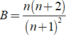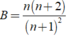Rút gọn biểu thức C=(1+1/3).(1+1/8).(1+1/16)...(1+1/n²+2n
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(3\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^2-1\right)\left(2^2+1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^4-1\right)\left(2^4+1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^8-1\right)\left(2^8+1\right)\left(2^{16}+1\right)\)
\(=\left(2^{16}-1\right)\left(2^{16}+1\right)\)
\(=2^{32}-1\)


\(A=\left(1+\frac{1}{3}\right).\left(1+\frac{1}{8}\right).\left(1+\frac{1}{15}\right)...\left(1+\frac{1}{n^2+2n}\right)\)
\(A=\frac{3+1}{3}.\frac{8+1}{8}.\frac{15+1}{15}...\frac{n^2+2n+1}{n^2+2n}\)
\(A=\frac{4}{3}.\frac{9}{8}.\frac{16}{15}...\frac{\left(n+1\right)^2}{n^2+2n}\)
\(A=\frac{2.2}{1.3}.\frac{3.3}{2.4}.\frac{4.4}{3.5}...\frac{\left(n+1\right)^2}{n.\left(n+2\right)}\)
\(A=\frac{2.3.4...\left(n+1\right)}{1.2.3...n}.\frac{2.3.4...\left(n+1\right)}{3.4.5...\left(n+2\right)}\)
\(A=\left(n+1\right).\frac{2}{n+2}=\frac{2.\left(n+1\right)}{n+2}\)
Ta có : \(1+\frac{1}{k^2+2k}=\frac{k^2+2k+1}{k^2+2k}=\frac{\left(k+1\right)^2}{k\left(k+2\right)}\) với k thuộc N*
Áp dụng với k = 1,2,3,....,n được :
\(A=\left(1+\frac{1}{3}\right)\left(1+\frac{1}{8}\right)\left(1+\frac{1}{15}\right)...\left(1+\frac{1}{n^2+2n}\right)\)
\(=\frac{\left(1+1\right)^2}{1.\left(1+2\right)}.\frac{\left(2+1\right)^2}{2.\left(2+2\right)}.\frac{\left(3+1\right)^2}{3.\left(3+2\right)}...\frac{\left(n+1\right)^2}{n.\left(n+2\right)}\)
\(=\frac{\left[2.3.4...\left(n+1\right)\right]^2}{1.2.3...n.3.4.5...\left(n+2\right)}=\frac{\left[\left(n+1\right)!\right]^2}{n!.\frac{\left(n+2\right)!}{2}}\)

Ta có: \(\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)\)
\(=\dfrac{\left(3-1\right)\left(3+1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{\left(3^4-1\right)\left(3^4+1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{\left(3^8-1\right)\left(3^8+1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{\left(3^{16}-1\right)\left(3^{16}+1\right)}{2}\)
\(=\dfrac{3^{32}-1}{2}\)
Rút gọn: (3 + 1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(3 + 1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(3-1)(3 + 1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(32-1)(32 + 1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(34-1)(34 + 1)(38 + 1)(316 + 1)(332 + 1)
A=(38-1)(38 + 1)(316 + 1)(332 + 1)
A=(316-1)(316 + 1)(332 + 1)
A=(332 - 1)(332 + 1)
A=364-1
=>A=(364-1) /2

\(A=\frac{1}{1\left(2n-1\right)}+\frac{1}{3\left(2n-3\right)}+...+\frac{1}{\left(2n-1\right).1}\)
\(A=\frac{1}{2n}\left[\frac{2n-1+1}{1\left(2n-1\right)}+\frac{2n-3+3}{3\left(2n-3\right)}+...+\frac{1+2n-1}{\left(2n-1\right).1}\right]\)
\(A=\frac{1}{2n}\left[\frac{1}{1}+\frac{1}{2n-1}+\frac{1}{3}+\frac{1}{2n-3}+...+\frac{1}{2n-1}+\frac{1}{1}\right]\)
\(A=\frac{1}{n}\left(1+\frac{1}{3}+\frac{1}{5}+...+\frac{1}{2n-3}+\frac{1}{2n-1}\right)\)
\(\Rightarrow\frac{a}{b}=\frac{1}{n}\).

\(P=12\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(=\dfrac{\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)}{2}\)
\(=\dfrac{\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)}{2}\)
\(=\dfrac{\left(5^{16}-1\right)\left(5^{16}+1\right)}{2}\)
\(=\dfrac{5^{32}-1}{2}\)
\(P=12\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\)
\(2P=\left(5^2-1\right)\left(5^2+1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{32}+1\right)\)
\(2P\)\(=\left(5^4-1\right)\left(5^4+1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)\)
\(2P=\)\(\left(5^8-1\right)\left(5^8+1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)\)
\(2P=\left(5^{16}-1\right)\left(5^{16}+1\right)\left(5^{32}+1\right)\)
\(2P=5^{32}-1\)
\(P=\dfrac{5^{32}-1}{2}\)