Tìm các hằng số a; b sao cho:
a)x\(^4\)+ax\(^2\)+b chia hết cho x\(^2\)-x+1
b)ax\(^3\)+bx\(^2\)+5x-50 chia hết cho x\(^2\)+3x-10
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Biểu thức x ( a 2 - a b + b 2 + y ) có các biến là x, y
Chọn đáp án C

\(ax^3-2x^3+x=\left(a-2\right)x^3+x\)
- Với \(a=2\Rightarrow\) đa thức trở thành \(x\) có bậc 1
- Với \(a\ne2\Rightarrow\) đa thức có bậc 3
Vậy đa thức có bậc 1 nếu \(a=2\) và có bậc 3 nếu \(a\ne2\)

Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
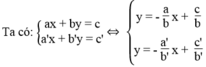
Hệ phương trình có vô số nghiệm khi hai đường thẳng trùng nhau. Nghĩa là hai đường thẳng có hệ số góc và tung độ gốc bằng nhau:
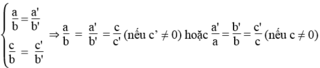
*a = 0, a’ ≠ 0
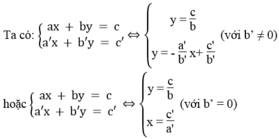
Vì hai đường thẳng 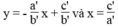 luôn luôn cắt trục hoành còn đường thẳng y = c/b song song hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
luôn luôn cắt trục hoành còn đường thẳng y = c/b song song hoặc trùng với trục hoành nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*a = a’ = 0
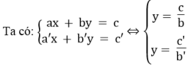
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
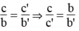
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
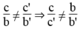
*b = 0, b’ ≠ 0
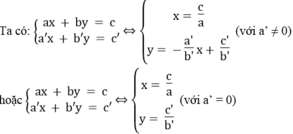
Vì hai đường thẳng 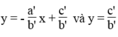 luôn luôn cắt trục tung còn đường thẳng x = c/a song song hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
luôn luôn cắt trục tung còn đường thẳng x = c/a song song hoặc trùng với trục tung nên chúng luôn luôn cắt nhau.
Vậy hệ phương trình chỉ có một nghiệm duy nhất.
*b = b’ = 0
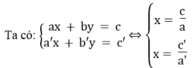
Hệ có vô số nghiệm khi hai đường thẳng trùng nhau, nghĩa là:
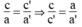
Hệ vô nghiệm khi hai đường thẳng song song nhau, nghĩa là:
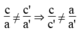
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn có vô số nghiệm:
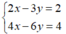
Vì 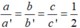 nên hệ phương trình có vô số nghiệm
nên hệ phương trình có vô số nghiệm

Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
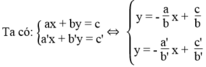
Hệ phương trình vô nghiệm khi hai đường thẳng song song nhau. Nghĩa là hai đường thẳng có hệ số góc bằng nhau và tung độ gốc khác nhau:
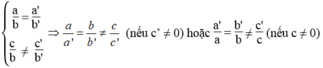
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
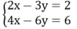
Vì 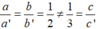 nên hệ phương trình trên vô nghiệm
nên hệ phương trình trên vô nghiệm


Xét các trường hợp:
1. a, b, a’, b’ ≠ 0
Ta có:
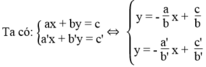
Hệ phương trình có một nghiệm duy nhất khi hai đường thẳng cắt nhau. Nghĩa là hai đường thẳng có hệ số góc khác nhau:
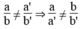
Áp dụng:
Hệ hai phương trình bậc nhất hai ẩn vô nghiệm:
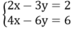
Vì 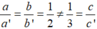 nên hệ phương trình trên vô nghiệm
nên hệ phương trình trên vô nghiệm

\(=3a^2x^6y^4\cdot x^2y^2\cdot2ay^3z=6a^3\cdot x^8y^9z\)
Bậc là 18
Ta có:(3a2x6y4).(-x2y2).(-2ay3z)
=(3\(a^2\).2a).(\(x^6.x^2\)).(\(y^4.y^2.y^3\)).z (với a là hằng số khác 0)
=6\(a^3x^8y^7z\)
Bậc của đơn thức là 8+7+1=16 (với a là hằng số khác 0)
a) Đặt f(x) = x4 + ax2 + b
g(x) = x2 - x + 1
h(x) là thương trong phép chia f(x) cho g(x)
Ta có : f(x) bậc 4 ; g(x) bậc 2 => h(x) bậc 2
=> h(x) có dạng x2 + cx + d
f(x) chia hết cho g(x) <=> f(x) = g(x).h(x)
<=> x4 + ax2 + b = ( x2 - x + 1 )( x2 + cx + d )
<=> x4 + ax2 + b = x4 + cx3 + dx2 - x3 - cx2 - dx + x2 + cx + d
<=> x4 + ax2 + b = x4 + ( c - 1 )x3 + ( d - c + 1 )x2 + ( c - d )x + d
Đồng nhất hệ số ta có :
c - 1 = 0 ; a = d - c + 1 ; c - d = 0 ; b = d
=> a = b = c = d = 1
Vậy a = b = 1
b) Đặt f(x) = ax3 + bx2 + 5x - 50
g(x) = x2 + 3x - 10 = x2 - 2x + 5x - 10 = x( x - 2 ) + 5( x - 2 ) = ( x - 2 )( x + 5 )
f(x) chia hết cho g(x) <=> ax3 + bx2 + 5x - 50 chia hết cho ( x - 2 )( x + 5 )
=> \(\hept{\begin{cases}\left(ax^3+bx^2+5x-50\right)⋮\left(x-2\right)\left[1\right]\\\left(ax^3+bx^2+5x-50\right)⋮\left(x+5\right)\left[2\right]\end{cases}}\)
Áp dụng định lí Bézout vào [ 1 ] ta có :
f(x) chia hết cho ( x - 2 ) <=> f(2) = 0
=> 8a + 4b + 10 - 50 = 0
=> 8a + 4b = 40
=> 2a + b = 10 (1)
Áp dụng định lí Bézout vào [ 2 ] ta có :
f(x) chia hết cho ( x + 5 ) <=> f(-5) = 0
=> -125a + 25b - 25 - 50 = 0
=> -125a + 25b = 75
=> -5a + b = 3 (2)
Từ (1) và (2) => \(\hept{\begin{cases}2a+b=10\\-5a+b=3\end{cases}}\Rightarrow\hept{\begin{cases}a=1\\b=8\end{cases}}\)
Vậy ...