(AI GIẢ NHANH SẼ ĐƯỢC TICK NHIỀU)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 2
Xếp 4 bạn nữ: có \(4!\) cách
4 bạn nữ tạo ra 5 khe trống, xếp 2 bạn nam vào 5 khe trống đó: \(A_5^2\) cách
Vậy tổng cộng có \(4!.A_5^2\) cách xếp thỏa mãn
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 2
1. Đã giải
2.
Xếp 10 cái bánh thành hàng ngang, 10 cái bánh tạo ra 9 khe trống (mà khe trống này nằm giữa 2 cái bánh)
Đặt 2 vách ngăn vào 9 vị trí nói trên, 2 vách ngăn sẽ chia 10 cái bánh làm 3 phần sao cho mỗi phần có ít nhất 1 cái bánh. Vậy có \(C_9^2\) cách đặt 2 vách ngăn hay có \(C_9^2\) cách chia 10 cái bánh cho 3 người sao cho mỗi người có ít nhất 1 cái bánh.
9 tháng 4 2023
n(Ω)=6!
A:" Xếp thành 1 dãy hàng ngang sao cho 2 bạn học sinh nam đứng cạnh nhau"⇒ \(\overline{A}\):" 2 bạn học sinh nam ko đứng cạnh nhau".
Ghép 2 bạn học sinh nam thành 1 nhóm⇒ coi còn 5 người⇒ n(A)=2*5!( do hoán vị 2 bạn nam, và xếp 5 người)⇒ n(\(\overline{A}\))=6!-2*5!=4*5!
NV
Nguyễn Việt Lâm
Giáo viên
22 tháng 12 2022
Xếp Phúc Đức cạnh nhau có \(2!\) cách
Xếp 4 học sinh nữ có \(4!\) cách
4 học sinh nữ tạo ra 5 khe trống, xếp cặp Phúc-Đức và 3 học sinh nam còn lại vào 5 khe trống này có: \(A_5^4\) cách
\(\Rightarrow2!.4!.A_5^4\) cách xếp thỏa mãn
12 tháng 4 2023
a: SỐ cách xếp là;
5!*6!*2=172800(cách)
b: Số cách xếp là \(6!\cdot5!=86400\left(cách\right)\)
CM
2 tháng 9 2019
- Nếu đánh số theo hàng dọc từ 1 đến 9 thì cần xếp 5 học nữ vào 5 vị trí lẻ nên có 5!cách xếp; và xếp 4 học sinh nam vào 4 vị trí chẵn nên có 4!cách xếp. Theo quy tắc nhân ta có, ta có 4!*5! Cách xếp 9 học sinh thành hàng dọc xen kẽ nam nữ.
Chọn A
CM
24 tháng 12 2019
Chọn D
Số phần tử của không gian mẫu: 
Gọi A là biến cố: “cặp sinh đôi ngồi cạnh nhau và nam nữ không ngồi đối diện nhau”.
Ta tính n() như sau:
Đánh số các ghế ngồi của 8 học sinh như hình vẽ sau:
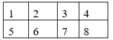
- Để xếp cho cặp sinh đôi ngồi cạnh nhau có 6 cách.
- Mỗi cách như vậy có cách đổi chỗ.
- Với mỗi cách xếp cặp sinh đôi, ví dụ: Cặp sinh đôi ở vị trí 1 và 2.
Do nam nữ không ngồi đối diện nên:
+ Vị trí 5 và 6 đều có 3 cách.
+ Vị trí 3 có 4 cách, vị trí 7 có 1 cách.
+ Vị trí 4 có 2 cách, vị trí 8 có 1 cách.
Suy ra n(A) = 6.2.3.3.4.1.2.1 = 864
CM
14 tháng 4 2018
Chọn B.
Phương pháp: Sử dụng hoán vị và quy tắc nhân.
Cách giải: Xếp 12 học sinh vào 12 ghế có 12! cách xếp.
Đánh số ghế như sau:
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Chọn giới tính nam hoặc nữ có 2 cách.
Xếp nam hoặc nữ ngồi vào các ghế 1, 3, 5, 8, 10,12 có 6!= 720 cách.
Xếp các bạn giới tính còn lại vào 6 ghế còn lại có 6!= 720cách.
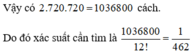
Nam Nữ Nữ Nam Nữ Nữ
Nữ nữ nam nữ nữ nam nữ nữ