điền Đ hay S
Hai đg thẳng cắt nhau thì ko song vs nhau
Một tam giác có thể có hai góc vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 10 2019
Câu đúng: a) và g).
Câu sai: b), c), d), e), f), h).
Giải thích:
- Câu b sai vì nếu ba điểm( phân biệt) cho trước là ba điểm thẳng hàng thì có đúng 1 đường thẳng đi qua ba điểm đó.
- Câu c sai vì nếu bốn điểm ( phân biệt) cho trước là bốn điểm thẳng hàng thì có đúng 1 đường thẳng đi qua bốn điểm đó.
- Câu d sai vì hai đường thẳng phân biệt có thể song song hoặc cắt nhau.
- Câu e sai vì hai đường thẳng không cắt nhau có thể trùng nhau hoặc song song.
- Câu f sai vì hai đường thẳng không song song có thể có thể trùng nhau hoặc cắt nhau.
- Câu h sai vì ba đường thẳng phân biệt, đôi một cắt nhau thì có thể có đúng 1 giao điểm. Như hình vẽ dưới đây.
6 tháng 12 2016
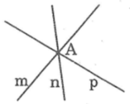
Ta có hình vẽ:
A B C M E F N x y
Câu d mình quên kí hiệu vuông góc rồi, bạn tự bổ sung nhé
a/ Xét tam giác AMB và tam giác AMC có:
AB = AC (GT)
BM = MC (GT)
AM : cạnh chung
=> tam giác AMB = tam giác AMC (c.c.c)
b/ Xét tam giác AEM và tam giác AFM có:
\(\widehat{E}\)=\(\widehat{F}\)=900
AM : cạnh chung
\(\widehat{EAM}\)=\(\widehat{FAM}\) ( vì tam giác AMB = tam giác AMC)
Vậy tam giác AEM = tam giác AFM (g.c.g)
=> AE = AF (2 cạnh tương ứng)
c/ Xét tam giác EBM và tam giác FCM có:
\(\widehat{E}\)=\(\widehat{F}\)=900
BM = MC (GT)
\(\widehat{B}\)=\(\widehat{C}\) (vì tam giác ABC cân có AB = AC)
Vậy tam giác EBM = tam giác FCM
(theo trường hợp cạnh huyền góc nhọn)
=> BE = FM (2 cạnh tương ứng) (1)
Ta có: EM: cạnh chung (2)
Ta có: 2 tam giác AEM và tam giác AFM đối xứng qua cạnh chung AM và có: \(\widehat{E}\)=\(\widehat{F}\)=900
=> \(\widehat{EMF}\) = 900 = \(\widehat{BEM}\) (3)
Từ (1),(2),(3) => tam giác BEM = tam giác EFM
=> \(\widehat{FEM}\)=\(\widehat{EMB}\) (2 góc tương ứng)
Mà 2 góc này đang ở vị trí so le trong
=> EF // BC
d/ Xét tam giác ABN và tam giác ACN có:
AB = AC (GT)
\(\widehat{BAN}\)=\(\widehat{CAN}\) (vì tam giác AMB = tam giác AMC)
AN: chung
=> tam giác ABN = tam giác ACN (c.g.c)
BN = CN ( 2 cạnh tương ứng)
Xét tam giác BMN và tam giác CMN có:
MN: chung
BM = MC (GT)
BN = CN (đã chứng minh)
=> tam giác BMN = tam giác CMN (c.c.c)
-Ta có: tam giác ABM = tam giác ACM (câu a)
=> \(\widehat{AMB}\)=\(\widehat{AMC}\) (2 góc tương ứng)
Mà \(\widehat{AMB}\)+\(\widehat{AMC}\) = 1800 (kề bù)
=> góc AMB = góc AMC = 900
-Ta có: tam giác BMN = tam giác CMN (đã chứng minh)
=> \(\widehat{BMN}\)=\(\widehat{CMN}\) (2 góc tương ứng)
mà \(\widehat{BMN}\)+\(\widehat{CMN}\)=1800 (kề bù)
=> góc BMN = góc CMN = 900
Ta có: \(\widehat{AMB}\)+\(\widehat{BMN}\)=900+900 = 1800
hay \(\widehat{AMC}\)+\(\widehat{CMN}\)=900+900 = 1800
hay A,M,N thẳng hàng
4 tháng 10 2017
A B C D E 35 35 35 110 Có AD là tia phân giác góc BAC => Góc BAD = góc BAC/2=70/2=35 độ
có BE // AD => góc BAD= góc ABE = 35 độ ( so le trong )
Có góc BAC + góc BAE = 180 độ ( kề bù )
=> góc BAE = 180 độ - góc BAC = 180 - 70 = 110 độ
Có BAE + ABE + AEB = 180 độ ( tổng 3 góc tam giác AEB )
=> AEB = 180 - BAE - ABE = 180 -110-35=35 độ
11 tháng 10 2018
ABI=HBC( 2 góc đồng vị ,AI // BH )
mà ABH =HBC ( BH là tia phân giác của ABC )
=> ABI=ABH
mà AHB =BAI (2 góc so le trong,AI //BH )
=> AIB = BAI
=> tam giác BAI cân tại B
mà BK là tia phân giác của ABI của tam giác BAI cân tại B
=> BK là đường cao của tam giác BAI
=> BK _I_AI
a) Đ
b) S
đ
S
MK nghĩ thế ! Sai thì ko mk nhé !