Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a, Vì M,N là trung điểm AB,AC nên MN là đtb tg ABC
Do đó MN//BC
b, Vì MN là đtb tg ABC nên \(MN=\dfrac{1}{2}BC=6\left(cm\right)\)
c, Vì MN//BC nên BMNC là hình thang

* Xét tam giác ABC có D và E lần lượt là trung điểm của AB và AC nên DE là đường trung bình của tam giác.
Suy ra: DE// BC và
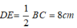
* Xét tứ giác DECB có DE // BC nên DECB là hình thang.
Lại có: M và N lần lượt là trung điểm của BD và EC nên MN là đường trung bình của hình thang .

Chọn đáp án D

D và E là trung điểm của AB và AC => DE là đường trung bình của tam giác ABC
=> DE//BC và DE=1/2 BC = 9cm
Tứ giác DECB có DE // BC => Hình thang DECB đáy DE, CB
Lại có M, N là trung điểm BD và CE=> MN là đường trung bình của hình thang DECB
=> MN = 1/2 ( DE + BC) = 1/2 (9+18) = 13,5 (cm)
Vậy....................................
________________________JK~ Liên Quân Group ________________________

a: Ta có: ΔABC vuông tại A
mà AP là đường trung tuyến
nên \(AP=\dfrac{BC}{2}=5\left(cm\right)\)
Xét ΔABC có
M,N lần lượt là trung điểm của AB,AC
=>MN là đường trung bình của ΔABC
=>MN//BC và \(MN=\dfrac{1}{2}BC\)
=>\(MN=\dfrac{1}{2}\cdot10=5\left(cm\right)\)
b: Xét ΔABC có
N,P lần lượt là trung điểm của CA,CB
=>NP là đường trung bình của ΔABC
=>NP//AB và \(NP=\dfrac{AB}{2}\)
Ta có: NP//AB
M\(\in\)AB
Do đó: NP//AM
ta có: \(NP=\dfrac{AB}{2}\)
\(AM=\dfrac{AB}{2}\)=MB
Do đó; NP=AM=MB
Xét tứ giác AMPN có
AM//NP
AM=NP
Do đó: AMPN là hình bình hành
Hình bình hành AMPN có \(\widehat{MAN}=90^0\)
nên AMPN là hình chữ nhật

Vì M là trung điểm AB
N là trung điểm AC
=> MN là đường trung bình tam giác ABC
=> MN // BC ; MN = 1/2 BC
=> \(MN=\frac{BC}{2}=\frac{20}{2}=10\)cm
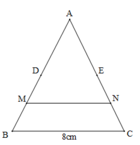

Tam giác ABC có : AM = MB
AN = NC
=> MN là đường trung bình của tam giác ABC
=> MN = 1/2 BC
=> BC = 2MN = 2.7=14
#Hoctot
Nối M với N ta được đoạn thẳng MN
Ta có : M là trung điểm của AB
N là trung điểm của AC
=> MN là đường trung bình của tam giác ABC
=> MN // BC và MN = 1/2BC
<=> 7 = 1/2BC
<=> BC = 14cm