trên hình 11 cho biết tứ giác ABCD là Hình bình hành .Chứng minh rằng a) EGFH là hình bình hành b)Các đường thẳng AC,BD,EF,GH đồng qui
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
6 tháng 12 2022
Bài 2:
a: Xét ΔADN vuông tại N và ΔCBM vuông tại M có
AD=CB
góc ADN=góc CBM
DO đó: ΔADN=ΔCBM
=>DN=BM và AN=CM
b: Xet tứ giác AMCN có
AN//CM
AN=CM
Do đó: AMCN là hình bình hành
c: Gọi O là giao của AC và BD
=>O là trung điểm của AC
Xet ΔAKC có AN/AK=AO/AC
nên NO//KC
=>KC//BD
Xét ΔBAK có
BN vừa là đường cao, vừa là trung tuyến
nên ΔBAK cân tại B
=>BA=BK=DC
Xét tứ giác BDKC có
KC//BD
DC=BK
Do đo; BDKC là hình thang cân
6 tháng 12 2022
Bài 2:
a: Xét ΔADN vuông tại N và ΔCBM vuông tại M có
AD=CB
góc ADN=góc CBM
DO đó: ΔADN=ΔCBM
=>DN=BM và AN=CM
b: Xet tứ giác AMCN có
AN//CM
AN=CM
Do đó: AMCN là hình bình hành
c: Gọi O là giao của AC và BD
=>O là trung điểm của AC
Xet ΔAKC có AN/AK=AO/AC
nên NO//KC
=>KC//BD
Xét ΔBAK có
BN vừa là đường cao, vừa là trung tuyến
nên ΔBAK cân tại B
=>BA=BK=DC
Xét tứ giác BDKC có
KC//BD
DC=BK
Do đo; BDKC là hình thang cân
28 tháng 5 2022
a: Xét tứ giác AHCG có
AG//CH
AG=CH
Do đó: AHCG là hình bình hành
b: Xét ΔAEG và ΔCFH có
AE=CF
\(\widehat{A}=\widehat{C}\)
AG=CH
Do đó: ΔAEG=ΔCFH
Suy ra: EG=FH
Xét ΔEBH và ΔFDG có
EB=FD
\(\widehat{B}=\widehat{D}\)
BH=DG
DO đó: ΔEBH=ΔFDG
Suy ra: EH=FG
Xét tứ giác EHFG có
EH=FG
EG=HF
Do đó: EHFG là hình bình hành
c: ta có: ABCD là hình bình hành
nên Hai đường chéo AC và BD cắt nhau tại trung điểm của mỗi đường(1)
Ta có: AECF là hình bình hành
nên hai đường chéo AC và EF cắt nhau tại trung điểm của mỗi đường(2)
Ta có: EHFG là hình bình hành
nên Hai đường chéo EF,HG cắt nhau tại trung điểm của mỗi đường(3)
Từ (1), (2) và (3) suy ra AC,BD,GH,EF đồng quy
KV
10 tháng 11 2023
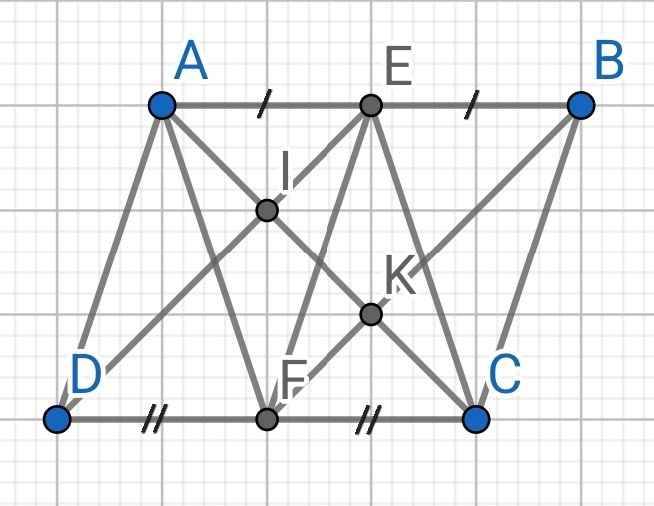a) Do ABCD là hình bình hành (gt)
⇒ AB = CD (1)
Do E là trung điểm AB (gt)
⇒ AE = BE = AB : 2 (2)
Do F là trung điểm CD (gt)
⇒ CF = DF = CD : 2 (3)
Từ (1), (2) và (3)
⇒ AE = BE = CF = DF
Do ABCD là hình bình hành (gt)
⇒ AB // CD
⇒ AE // CF
Tứ giác AECF có:
AE // CF (cmt)
AE = CF (cmt)
⇒ AECF là hình bình hành
b) Do AB // CD (cmt)
⇒ BE // DF
Tứ giác BEDF có:
BE // DF (cmt)
BE = DF (cmt)
⇒ BEDF là hình bình hành
⇒ BF // DE
⇒ BK // EI và KF // DI
∆CDI có:
F là trung điểm CD (gt)
KF // DI (cmt)
⇒ K là trung điểm của CI
⇒ CK = IK (4)
∆ABK có:
E là trung điểm của AB (gt)
BK // EI (cmt)
⇒ I là trung điểm của AK
⇒ AI = IK (5)
Từ (4) và (5)
⇒ AI = IK = KC
11 tháng 10 2021
a: Xét tứ giác EBDA có
EB//DA
EA//DB
Do đó: EBDA là hình bình hành
Xét tứ giác ABDF có
AB//DF
AF//BD
Do đó: ABDF là hình bình hành
where is hình?