Cho hình bình hành ABCD có BC=2AB và \(\widehat{A}\)=60\(^0\)Gọi E, F theo thứ tự là trung điểm của BC và AD
a)ECDF là hình gì
b)ABED là hình gì
c)Tính số đo góc AED
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét tứ giác ECDF có
EC//DF
EC=DF
Do đó: ECDF là hình bình hành
mà EC=CD
nên ECDF là hình thoi

a) Ta sẽ có FD//EC và FD = EC = 0.5 AD Þ ECDF là hình bình hành.
Mà A B 1 2 B C
Þ AB = BE = EF = EC
Þ CDFE là hình thoi.
b) Tứ giác ABED là hình thang cân vì BE//AD và B A D ^ = A D E ^ = 60 0
c) Ta có E F = C D = A B = 1 2 C D = 1 2 A D , F là trung điểm AD Þ A E D ^ = 90 0
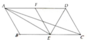

a, Ta có :
EC // FD
\(EC=FD=\frac{4}{2}BC=\frac{1}{2}AD\)
=> ECDF là hình bình hành
\(EF=AB=\frac{1}{2}BC\)
=> ECDF là hình thoi
b, \(\widehat{A} =60^o\)
\(\Rightarrow D=120^o\)
\(\Rightarrow\widehat{EDF}=120^o:2=60^o\)
Mà BE // AD
==> BEDA là hình thang cân
c, Xét tam giác AFE : AF = EF --- > góc AFE
BEFA là hình thoi
==> AE là tia phân giác của \(\widehat{BAE}\Rightarrow\widehat{EAF}=30^o\)
Mà EDA = 60o
=> Trong tam giác EAD = 180o = \(\widehat{EAF}+\widehat{ADE}+\widehat{EAD}\)
\(=30^o+60^o+\widehat{EAD}\)
\(\Rightarrow\widehat{AED}=60^o\)