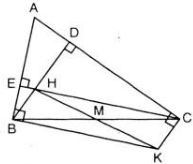
Cho tam giác nhọn ABC, các đường cao BD, CE cắt nhau tại H. Đường vuông góc với AB tại B và đường vuông góc với AC tại C cắt nhau tại K
a) CM AH vuông góc với BC
b) CM tứ giác BHCK là hình bình hành
c) Gọi I là trung điểm của AK, M là trung điểm của BC. CM 3 điểm H,M,K thẳng hàng và IM = AH : 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
28 tháng 7 2023
a: Xét ΔABC có
BD,CE là đường cao
BD cắt CE tại H
=>H là trực tâm
=>AH vuông góc BC
b: Xét tứ giác BHCK có
BH//CK
BK//CH
=>BHCK là hình bình hành
16 tháng 12 2023
a: ta có: BH\(\perp\)AC
CK\(\perp\)AC
Do đó: BH//CK
Ta có: CH\(\perp\)AB
BK\(\perp\)BA
Do đó: CH//BK
Xét tứ giác BHCK có
BH//CK
BK//CH
Do đó: BHCK là hình bình hành
b: Ta có: BHCKlà hình bình hành
=>BC cắt HK tại trung điểm của mỗi đường
mà M là trung điểm của BC
nên M là trung điểm của HK
=>H,M,K thẳng hàng
14 tháng 12 2023
a, Ta có:
- BH là đường cao của tam giác ABC, nên BH vuông góc với AC.
- CK là đường cao của tam giác ABC, nên CK vuông góc với AB.
- Vì BH và CK đều vuông góc với hai cạnh AB và AC của tam giác ABC, nên BHCK là hình bình hành.
b, Gọi M là trung điểm của BC. Ta cần chứng minh CM, HM và KM thẳng hàng.
- Vì M là trung điểm của BC, nên BM = MC.
- Ta có BHCK là hình bình hành, nên BH = CK.
- Vì BH và CK là đường cao của tam giác ABC, nên BH = 2HM và CK = 2KM.
- Từ đó, ta có BM = MC = HM = KM.
- Vì BM = MC và HM = KM, nên CM, HM và KM thẳng hàng.
Vậy, ta đã chứng minh được CM, HM và KM thẳng hàng.
CM
14 tháng 3 2018
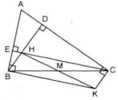
Ta có: CE ⊥ AB (gt)
KB ⊥ AB (gt)
⇒ BK // CE (1)
Tương tự BH // KC (2)
Từ (1) và (2) ⇒ BHCK là hình bình hành.
Gọi M là giao điểm của hai đường chéo BC và HK.
a) Tam giác ABC có hai đường cao BD và CE cắt nhau tại H nên H là trực tâm tam giác ABC
⇒ AH ⊥ BC. (3)
BHCK là hình thoi
⇔ HM ⊥ BC ( trong đó M là giao điểm của hai đường chéo HK và BC) (4)
Từ (3) và (4) suy ra: A, H, M thẳng hàng.
Khi đó,tam giác ABC có AM là đường cao đồng thời là đường trung tuyến nên tam giác ABC là cân tại A.
b) BHCK là hình chữ nhật
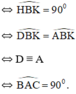
Vậy BHCK là hình chữ nhật khi tam giác ABC vuông tại A.
