3x2+14x-15=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
GH
12 tháng 9 2021
3x^2 + 14x + 15
= 3x^2 + 9x + 5x + 15
= 3x(x + 3) + 5(x + 3)
= (x + 3)(3x + 5)
LN
1
J
18 tháng 4 2019
a) \(3x^2-5x+2=0\)
Vì \(a+b+c=3-5+2=0\)
\(\Rightarrow\) pt co 2 ngiệm pb : \(x_1=1\) ; \(x_2=\frac{2}{3}\)
Vậy \(S=\left\{1;\frac{2}{3}\right\}\)
b) \(-3x^2+14x-8=0\)
\(\Delta'=7^2-\left(-3\right)\times\left(-8\right)=49-24=25\)
\(\Rightarrow\) pt có 2 nghiệm pb : \(x_1=4\) ; \(x_2=\frac{2}{3}\)
Vậy \(S=\left\{4;\frac{2}{3}\right\}\)
VD
2
12 tháng 9 2021
\(a,=5\left(x^3+8y\right)\\ b,=\left(4x+y\right)^2-16=\left(4x+y-4\right)\left(4x+y+4\right)\\ c,=3\left(x^2+2\cdot\dfrac{7}{3}x-5\right)\\ =3\left(x^2+2\cdot\dfrac{7}{3}x+\dfrac{49}{9}-\dfrac{94}{9}\right)\\ =3\left(x+\dfrac{7}{3}-\dfrac{\sqrt{94}}{3}\right)\left(x+\dfrac{7}{3}+\dfrac{\sqrt{94}}{3}\right)\)
12 tháng 9 2021
a: \(5x^3+40y=5\left(x^3+8y\right)\)
b: \(16x^2+8xy+y^2-16\)
\(=\left(4x+y\right)^2-16\)
\(=\left(4x+y-4\right)\left(4x+y+4\right)\)
TM
Tìm x:
a) x3 +3x2 - 10x = 0
b) x3 - 5x2 - 14x =0
c) x3 + 5x2- 24x =0
Giải giúp mình với ạ !
Mình cảm ơn !
4
NF
24 tháng 10 2017
x3+3x2-10x=0
=>x(3+3.2-10)=0
=>x=0
x3-5x2-14x=0
=>x(3-5.2-14)=0
=>x=0
x3+5x2-24x=0
=>x(3+5.2-24)=0
=>x=0
24 tháng 10 2017
Câu a)
\(x^3+3x^2-10=0\Rightarrow x\left(x^2+3x-10\right)=0\Rightarrow x\left(x^2-2x+5x-10\right)=0\Rightarrow x\left(x\left(x-2\right)+5\left(x-2\right)\right)=0\Rightarrow x\left(x+5\right)\left(x-2\right)=0\)
\(\Rightarrow x=0;x=5;x=2\)
CM
10 tháng 7 2018
Điều kiện x ≠ 0 và x ≠ -3
Ta có:
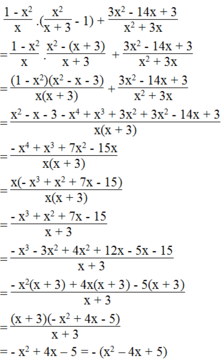
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên
- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.
Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x ≠ 0 và x ≠ -3
CM
17 tháng 10 2017
a) Phương trình bậc hai 4 x 2 + 4 x + 1 = 0
Có a = 4; b’ = 2; c = 1; Δ ’ = ( b ’ ) 2 – a c = 2 2 – 4 . 1 = 0
Phương trình có nghiệm kép là:
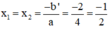
b) Phương trình 13852 x 2 – 14 x + 1 = 0
Có a = 13852; b’ = -7; c = 1;
Δ ’ = ( b ’ ) 2 – a c = ( - 7 ) 2 – 13852 . 1 = - 13803 < 0
Vậy phương trình vô nghiệm.
c) Phương trình bậc hai 5 x 2 – 6 x + 1 = 0
Có: a = 5; b’ = -3; c = 1.; Δ ’ = ( b ’ ) 2 – a c = ( - 3 ) 2 – 5 . 1 = 4 > 0
Phương trình có hai nghiệm phân biệt:
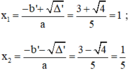
d) Phương trình bậc hai: 
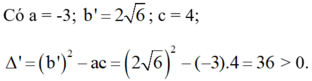
Phương trình có hai nghiệm phân biệt :
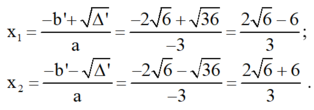
Kiến thức áp dụng
Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.
+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt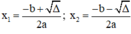 
+ Nếu Δ = 0, phương trình có nghiệm kép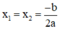 
;
+ Nếu Δ < 0, phương trình vô nghiệm.
DN
4
4 tháng 9 2021
\(3x^2-14x-5=3x\left(x-5\right)+\left(x-5\right)=\left(x-5\right)\left(3x+1\right)\)
\(3x^2+14x-15=0\)
\(\Delta=b^2-4ac=14^2-4\cdot3\cdot15=16\)
=> Phương trình có 2 nghiệm
\(=>\orbr{\begin{cases}x_1=\frac{-b+\sqrt{\Delta}}{2a}=\frac{-14+\sqrt{16}}{2\cdot3}=\frac{-10}{6}=\frac{-5}{3}\\x_2=\frac{-b-\sqrt{\Delta}}{2a}=\frac{-14-\sqrt{16}}{2\cdot3}=\frac{-18}{6}=-3\end{cases}}\)
Vậy...
Sai r babe :))
\(3x^2+14x-15=0\)
\(\Delta=14^2-4.3.\left(-15\right)=376\)
\(x_1=\frac{-14-\sqrt{376}}{28};x_2=\frac{-14+\sqrt{375}}{28}\)