Cho tam giác nhọn MNP. Gọi H là trực tâm của tam giác, I là trung điểm của NP. Trên tia HI lấy điểm điểm K sao cho IH= IK a. Chứng minh tứ giác NHPK là hình bình hành b. Chứng minh các tam giác MNK, MPK là các tam giác vuông c. Gọi O là trung điểm MK. Chứng minh rằng OM = ON= OP = OK và MH = 2.01
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 5 2015
bạn tự vẽ hỉnh nha
tg abe đều suy ra ae=eb=ab và bea=eba=eab=60 độ
tg acf đeu suy raac=cf=af và afc=fca=fac=60 độ
gọi gọi EN,AG,BM là đường cao của tg EBA VÀ CÁC ĐƯỜNG CAO CẮT NHAU TẠI TRỰC TÂM H
CMĐ TG ENB=ENA (CH GN) SUY RA NB=NA(2 CẠNG TƯƠNG ỨNG )
CMĐ TG HNB=HNA(C GC) SUY RA HB=HA(2 CẠNH TƯƠNG ỨNG ) (1)
CMĐ TG HIB=KIC (C G C) SUY RA HB=CK (2 CẠNH TƯƠNG ỨNG) VÀ GÓC HBI=KCI(2)
TỪ (1) VÀ (2) SUY RA HA=CK
CMĐ GÓC EBH=ABH=30 ĐỘ HAN
TA CÓ KCF+ACF+ACB+ICK=360
KCF =360-ACF-ACB-ICK =360-60-ACB-HBI=300-ACB-IBH(3)
TA CÓ GÓC HAF =HAB+BAC+CAF=30+BAC+60=90+BAC = 90+(180-ABC-ACB)=270-ABC-ACB=270-(IBH-30)-ACB =270-IBH+30-ACB=300-ACB-IBH(4)
TỪ (3) VÀ (4) TA SUY RA DC GÓC HAF=KCF
CMĐ TG HAF=KCF(C G C)
CHỖ NÀO BN KO HIỂU Ở BÀI MÌNH TRÌNH BÀY BN CÓ THỂ HỎI MÌNH .TAB CHO MÌNH NẾU ĐÚNG NHA
4 tháng 5 2017
chỗ cậu chứng minh các tam giác bằng nhau thì hơi dài.Cậu nên áp dụng t/c tam giác đều:
Có H là trực tâm của tam giác ABE
Mà tam giác ABE đều => H cũng là trọng tâm
=> BN=NA ( t/c đường trung tuyến )
MÀ EN vuông góc với AB ( Cách vẽ),BN=NA (cnt)=>N thuộc đường trung trực AB=>AH=BH ( t/c)
31 tháng 10 2021
a: Xét tứ giác BHCI có
E là trung điểm của BC
E là trung điểm của HI
Do đó: BHCI là hình bình hành
KV
1 tháng 11 2023
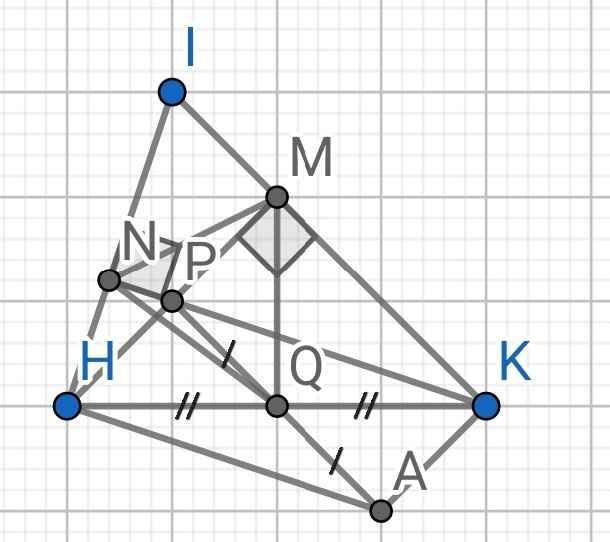a) Do PQ = QA (gt)
⇒ Q là trung điểm của AP
Tứ giác PHAK có:
Q là trung điểm của AP (cmt)
Q là trung điểm của HK (gt)
⇒ PHAK là hình bình hành
b) Do PHAK là hình bình hành (cmt)
⇒ PK = AH
c) ∆HNK vuông tại N
Q là trung điểm của HK (gt)
⇒ NQ là đường trung tuyến ứng với cạnh huyền HK
⇒ NQ = HK : 2 (1)
∆HMK vuông tại M
Q là trung điểm HK (gt)
⇒ MQ là đường trung tuyến ứng với cạnh huyền HK
⇒ MQ = HK : 2 (2)
Từ (1) và (2) ⇒ MQ = NQ
∆MNQ có:
MQ = NQ (cmt)
⇒ ∆MNQ cân tại Q
KN
6 tháng 10 2020
a) Vì H' đối xứng với H qua BC nên BC là đường trung trực của HH' => BH = BH', CH = CH'
Xét ∆BHC và ∆BH'C có:
BH = BH' (cmt)
BC: cạnh chung
HC = H'C (cmt)
Do đó ∆BHC = ∆BH'C (c.c.c)
b) Gọi T là giao điểm của HH' với BC
∆HH'K có T là trung điểm của HH' (gt) và HI = IK (gt) nên TI là đường trung bình của tam giác => HI // H'K hay BC // H'K
Dễ chứng minh: ∆HIB = ∆KIC (c.g.c) => ^HBI = ^KCI (hai góc tương ứng)
Mà ^HBI = ^H'BC (∆BHC = ∆BH'C) nên ^H'BC = ^KCI
Hình thang BH'KC có ^H'BC = ^KCI nên là hình thang cân (đpcm)