Cho tam giác MNP vuông tại N, I là trung điểm MP. Kẻ ID vuông góc MN tại D. IE vuông góc NP tại E
a)NDIE là hình gì
b)MIED là hình gì
c)Trên tia đối của tia IE lấy H sao cho IE=IH. C/m MEPH là hình bình hành. Từ đó suy ra MH=EP
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
5 tháng 1 2022
a: Xét tứ giác MKIE có
\(\widehat{MKI}=\widehat{MEI}=\widehat{EMK}=90^0\)
Do đó: MKIE là hình chữ nhật
b: Xét ΔMPN có
I là trung điểm của NP
IK//MP
Do đó: K là trung điểm của MN
Ta có: K là trung điểm của MN
mà IK⊥MN
nên IK là đường trung trực của MN
KV
27 tháng 10 2023
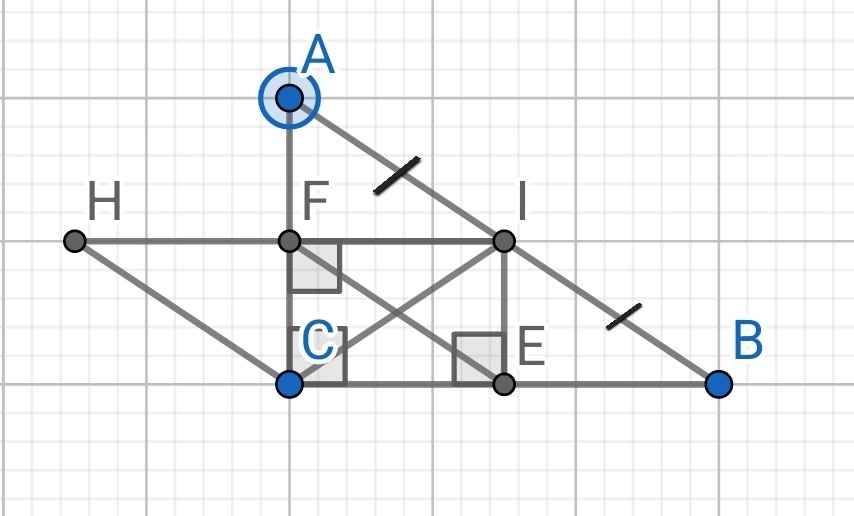*) Tứ giác CEIF là hình gì?
Tứ giác CEIF có:
∠CEI = ∠CFI = ∠ECF = 90⁰ (gt)
⇒ CEIF là hình chữ nhật
*) Do CEIF là hình chữ nhật (cmt)
⇒ FI = CE và FI // CE
Do FI // CE (cmt)
⇒ FH // CE
Do FI = CE (cmt)
FI = FH (gt)
⇒ FH = CE
Tứ giác CHFE có:
FH // CE (cmt)
FH = CE (cmt)
⇒ CHFE là hình bình hành
27 tháng 10 2023
Sửa đề: IF vuông góc AC tại F
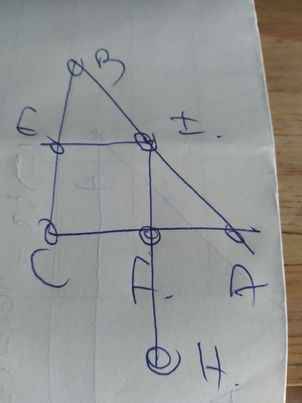
a: Xét tứ giác CEIF có
\(\widehat{CEI}=\widehat{CFI}=\widehat{FCE}=90^0\)
Do đó: CEIF là hình chữ nhật
b: CEIF là hình chữ nhật
=>CE//FI và CE=FI
CE=FI
FI=FH
Do đó: CE=FH
CE//FI
\(F\in IH\)
Do đó: CE=FH
Xét tứ giác CEFH có
CE//FH
CE=FH
Do đó: CEFH là hình bình hành
9 tháng 12 2019
a ) Xét ◇DENF có :
Góc N = Góc F = Ê = 90°
⇒◇DENF là hình chữ nhật
b ) Trong ΔMNP có : ND là đường trung tuyến
⇒ND = DP ( vì đường trung tuyến bằng nữa cạnh huyền )
Xét ΔNDF và ΔPDF có :
- ND = DP ( cmt )
- Góc NFD = Góc PFD ( = 90° )
- DF : cạnh chung
⇒ΔNDF = ΔPDF ( cạnh huyền - cạnh góc vuông )
⇒NF = PF ( 2 cạnh tương ứng )
⇒F là trung điểm NP
