1. Cho hình chữ nhật ABCD có AB=6cm, BC=8cm.Chứng minh rằng 4 điểm A,B,C,D thuộc cùng một đường tròn, tìm tâm và tính bán kính của đường tròn đó .2. Chứng minh các định lí sau:a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó thì tam giác đó vuôngAi giúp...
Đọc tiếp
1. Cho hình chữ nhật ABCD có AB=6cm, BC=8cm.Chứng minh rằng 4 điểm A,B,C,D thuộc cùng một đường tròn, tìm tâm và tính bán kính của đường tròn đó .
2. Chứng minh các định lí sau:
a) Tâm của đường tròn ngoại tiếp tam giác vuông là trung điểm của cạnh huyền.
b) Nếu một tam giác có một cạnh là đường kính của đường tròn ngoại tiếp tam giác đó thì tam giác đó vuông
Ai giúp với
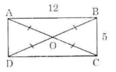
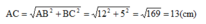
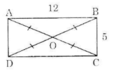
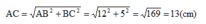
1/ Gọi O là giao hai đường chéo AC và BD
=> OA=OC; OB=OD (trong HCN hai đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có AC=BD (trong HCN hai đường chéo băng nhau)
=> OA=OC=OB=OD => 4 điểm A;B;C;D cùng nằm trên một đường tròn tâm O là giao của hai đường chéo HCN
2/
a/
Ta có tam giác ABC vuông tại A => BC là cạnh huyền, gọi O là trung điểm cạnh huyền => AO là trung tuyến thuộc cạnh huyền
=> OA=OB=OC=BC/2 (trong tg vuông trung tuyến thuộc cạnh huyền thì bằng nửa cạnh huyền) => O là tâm đường tròn ngoại tiếp tg ABC
b/
Ta có tg ABC có BC là đường kính đường tròn ngoại tiếp tg ABC => OA=OB=OC
+ Xét tg AOB có OA=OB => tg AOB cân tạo O => ^BAO = ^AOB (1)
+ Xét tg AOC có OA=OC => tg AOC cân tại O => ^CAO = ^AOC (2)
Xét tg ABC có
^ABC+^ABO+^ACO=180 (tổng các góc trong của 1 tg =180 độ)
=> (^BAO+^CAO)+^ABO+^ACO=180 (3)
Từ (1) (2) và (3) => ^ABC=^BAO+^CAO=^ABO+^ACO=180:2=90
=> tg ABC vuông tại A