Một bánh xe bán kính 60 (cm) quay đều vòng trong thời gian 2 (s). Tìm chu kì, tần số, tốc độ góc, tốc độ dài và gia tốc hướng tâm của nó?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HD
Hà Đức Thọ
Admin
10 tháng 10 2016
Chu kì là thời gian quay hết 1 vòng \(\Rightarrow T = \dfrac{2}{120}=\dfrac{1}{60}s\)
Tần số là số vòng quay trong 1 s \(\Rightarrow f= \dfrac{120}{2}=60(hz)\)
Tốc độ góc: \(\omega=\dfrac{2\pi}{T}=120\pi(rad/s)\)
Tốc độ dài: \(v=\omega.R = 120\pi.0,5=60\pi(m/s)\)
Gia tốc hướng tâm: \(a=\omega^2.R=(120\pi)^2.0,5=7200\pi^2(m/s^2)\)
10 tháng 10 2021
Bài 1.
Đường kính bánh xe: \(d=100cm=1m\) \(\Rightarrow R=0,5m\)
Điểm cách vòng bánh xe 1/5 bán kính xe: \(\Rightarrow R'=\dfrac{R}{5}=0,1m\)
Tốc độ góc ở điểm ngoài vòng bánh xe: \(\omega=\dfrac{v}{R}=\dfrac{10}{0,1}=100rad\)/s
Gia tốc hướng tâm tại điểm nằm ngoài bánh xe:
\(a_{ht}=\omega^2\cdot R'=100^2\cdot0,1=1000\)m/s2
VT
8 tháng 3 2017
Chọn C.
Đổi v = 40 km/h = 100/9 m/s.
Độ lớn gia tốc hướng tâm của xe bằng:
VT
4 tháng 3 2017
Chọn C.
Đổi v = 40 km/h = 100/9 m/s.
Độ lớn gia tốc hướng tâm của xe bằng:
VT
11 tháng 2 2018
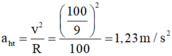
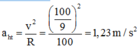
Chọn C.
Gia tốc rơi tự do ở độ cao h:
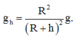
Lực hấp dẫn (trọng lực) đóng vai trò lực hướng tâm:
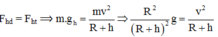
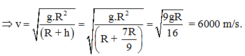
Chu kì của chuyển động tròn:
VT
22 tháng 10 2018
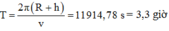
Từ biểu thức tính lực hướng tâm: F h t = m a h t = m v 2 r = m ω 2 r
Ta suy ra, khi bán kính quỹ đạo tăng gấp 2 lần so với trước và giảm tốc độ quay còn một nửa thì so với ban đầu, lực hướng tâm giảm đi 2 lần.
Đáp án: C
