Bài: Cho tam giác ABC \(\widehat{B}\) = 65o ; \(\widehat{C}\) = 65o. Kẻ tia Ax là tia đối của tia AB. Vẽ tia Ay song song với BC và tia Ay nằm giữa hai tia Ax, AC.a) Tính \(\widehat{BAC}\)b) Tính \(\widehat{BAy}\)c) Chứng minh tia Ay là tia phân giác...
Đọc tiếp
Bài: Cho tam giác ABC \(\widehat{B}\) = 65o ; \(\widehat{C}\) = 65o. Kẻ tia Ax là tia đối của tia AB. Vẽ tia Ay song song với BC và tia Ay nằm giữa hai tia Ax, AC.
a) Tính \(\widehat{BAC}\)
b) Tính \(\widehat{BAy}\)
c) Chứng minh tia Ay là tia phân giác của \(\widehat{xAC}\)
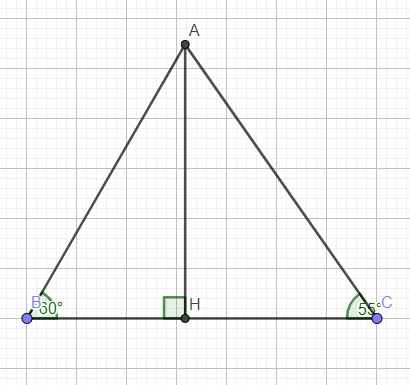
a) xét tam giác BAC ta có
B=65 độ
C=65 độ
=> tam giác ABC cân tại A
xét tam giác ABC ta có
B+C+A=180độ
=>65+65+A=180 độ
=>A=50 độ
b) vì Ay//Bc
mà góc C và góc CAy là 2 góc so le trong
=>C=CAy
mà góc C= 65 độ
=>CAy=65 độ
mà AC nằm giữa AB và Ay
=>BAC+CAy=BAy
=>BAy=65+50=115 dộ
c) vì góc BAy và góc xAy là 2 góc kề bù nên
=>BAy+xAy=180 độ
=>yAx=180-115=65 độ
mà Ay nằm giữa AC và Ax
mà CAy=xAy=65 độ
=>Ay là tia p/g của góc CAx
dit con me mày
vai lon luon dau cat moi