Cho tam giác ABC nhọn
Kẻ đường cao AH , từ H kẻ HE vuông góc với AB ( E thuộc AB )
Kẻ HF vuông AC ( F thuộc AC )
a) Chứng minh AE * AB = AF*AC
b) Biết AB =4 cm
AH = 3cm
Tính AE ; BE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
26 tháng 9 2021
a: Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AH^2=HB\cdot HC\left(1\right)\)
Xét ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB
nên \(AH^2=AE\cdot AB\left(2\right)\)
Xét ΔACH vuông tại H có HF là đường cao ứng với cạnh huyền AC
nên \(AH^2=AF\cdot AC\left(3\right)\)
Từ (1), (2) và (3) suy ra \(AE\cdot AB=AF\cdot AC=BH\cdot HC\)
7 tháng 10 2016
Xét ΔABH vuông tại H(gt)
=> \(AH^2=AE\cdot AB\) (1)
Xét ΔAHC vuông tại C(gt)
=>\(AH^2=AF\cdot AC\) (2)
Từ (1)(2) suy ra:
AE.AB=AF.AC
b) Xét ΔABH vuông tại H(gt)
=> \(AB^2=AH^2+BH^2=3^2+4^2=9+16=25\)
=>AB=25
Áp dụng hệ thức ta có:
\(AH^2=AE\cdot AB\)
=> \(AE=\frac{AH^2}{AB}=\frac{4^2}{5}=\frac{16}{5}\)
Có: AB=AE+BE
=>BE=AB-AE= \(5-\frac{16}{5}=\frac{9}{5}\)
K
22 tháng 10 2017
a) ta sẽ c/m 2 tam giác AFE và ABC đồng dạng
xét 2 tam giác trên ta có:
A^ chung ; AEF^ = ACB^ (cùng chắn cung AF của tứ giác nt AEHF)
=> 2 tam giác đồng dạng (g.g)
=> tỉ lệ => đẳng thức
b) tam giác vuông AHB : đường cao HE
=> AH^2 = AE * AB <=> AE = (AH)^2/ AB = .....thay vào.. (cm)
mặt khác: AB = AE+BE <=> BE = AB - AE = ...thay vào... (cm)
KL : AE = ....cm , BE = ...cm
3 tháng 8 2021
b) Xét ΔMEB và ΔMCF có
\(\widehat{MEB}=\widehat{MCF}\left(=\widehat{AEF}\right)\)
\(\widehat{M}\) chung
Do đó: ΔMEB\(\sim\)ΔMCF(g-g)
Suy ra: \(\dfrac{ME}{MC}=\dfrac{MB}{MF}\)
hay \(ME\cdot MF=MB\cdot MC\)
3 tháng 8 2021
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)(hai góc tương ứng)
CM
4 tháng 1 2019
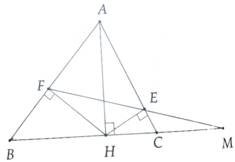
a, Ta có: ∆AEF ~ ∆MCE (c.g.c)
=> A F E ^ = A C B ^
b, Ta có: ∆MFB ~ ∆MCE (g.g)
=> ME.MF = MB.MC
3 tháng 8 2021
a) Áp dụng hệ thức lượng trong tam giác vuông vào ΔABH vuông tại H có HE là đường cao ứng với cạnh huyền AB, ta được:
\(AE\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HF là đường cao ứng với cạnh huyền AC, ta được:
\(AF\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
hay \(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)
Xét ΔAEF và ΔACB có
\(\dfrac{AE}{AC}=\dfrac{AF}{AB}\)(cmt)
\(\widehat{EAF}\) chung
Do đó: ΔAEF\(\sim\)ΔACB(c-g-c)
Suy ra: \(\widehat{AFE}=\widehat{ABC}\)
S
2 tháng 9 2017
a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)
30 tháng 5 2022
a: Xét ΔABH vuông tại H có HE là đường cao
nên \(AE\cdot AB=AH^2\left(1\right)\)
Xét ΔAHC vuông tại H có HF là đường cao
nên \(AF\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AE\cdot AB=AF\cdot AC\)
b: \(AB=\sqrt{3^2+4^2}=5\left(cm\right)\)
\(AE=\dfrac{AH^2}{AB}=\dfrac{4^2}{5}=3.2\left(cm\right)\)
BE=AB-AE=1,8(cm)
Bạn ơi, lần sau gửi câu hỏi đúng môn học nhé! Đây là toán mà!