cminh rằng với n tự nhiên khác 0: \(8\times2^n+2^{n+1}⋮5\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bước 1: Chứng minh công thức đúng cho n = 1. Khi n = 1, ta có: 1² = 1 = 1 . (1 + 1) . (2 . 1 + 1) / 6 = 1. Vậy công thức đúng cho n = 1.
Bước 2: Giả sử công thức đúng cho n = k, tức là 1² + 2² + ... + k² = k . (k + 1) . (2k + 1) / 6. Ta cần chứng minh công thức đúng cho n = k + 1, tức là 1² + 2² + ... + k² + (k + 1)² = (k + 1) . (k + 1 + 1) . (2(k + 1) + 1) / 6.
Bước 3: Chứng minh công thức đúng cho n = k + 1. Ta có: 1² + 2² + ... + k² + (k + 1)² = (k . (k + 1) . (2k + 1) / 6) + (k + 1)² = (k . (k + 1) . (2k + 1) + 6(k + 1)²) / 6 = (k . (k + 1) . (2k + 1) + 6(k + 1) . (k + 1)) / 6 = (k + 1) . ((k . (2k + 1) + 6(k + 1)) / 6) = (k + 1) . ((2k² + k + 6k + 6) / 6) = (k + 1) . ((2k² + 7k + 6) / 6) = (k + 1) . ((k + 2) . (2k + 3) / 6) = (k + 1) . ((k + 1 + 1) . (2(k + 1) + 1) / 6).
Vậy, công thức đã được chứng minh đúng cho mọi số tự nhiên n khác 0.


a: \(=5^{2003}\left(5^2-5+1\right)\)
\(=5^{2003}\cdot21⋮7\)

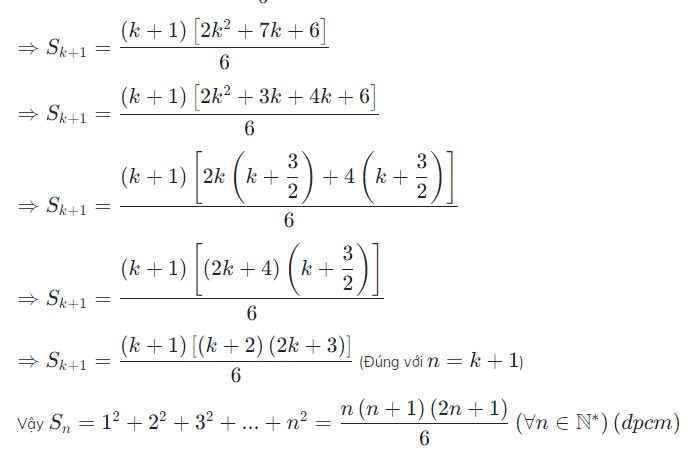
\(8.2^n+2^{n+1}=2^n\left(8+2\right)=2^n.10⋮10\)
ta có đpcm
8.2^n+2^n+1
=8.2^n+2^n.2
=10.2^n chia hết cho 5