Cho p nguyên tố. Hỏi có số chính phương nào viết được dưới dạng 2p + 3p không
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Ta có
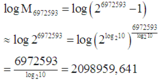
Do đó số chữ số của số đó là 2098959 + 1 = 2098960

Đáp án A
Ta có
log M 6972593 = log 2 6972593 − 1 ≈ log 2 6972593 = log 2 log 2 10 6972593 log 2 10 = 6972593 log 2 10 = 2098959 , 641
Do đó số chữ số của số đó là
2098959 + 1 = 2098960

Ta có:
6k+2=2(k+1) chia hết cho 2 nên là hợp số
Ta cũng có:
6k+3=3(k+1) chia hết cho 3 nên là hợp số
Vậy không có số nguyên tố nào được viết dưới dạng 6k+2 ; 6k+3 (k \(\in\) N )

mọi số tự nhiên chia cho 6 có số dư là 1,2,3,4,5
th1:k=0suy ra p=6k hợp số (loại)
th2 k=1suyra p= 6k+1
th3 k=2suy ra p=6k+2 (chọn)
th4 k=3suy ra p=6k+3 (chọn)
vậy p có dạng 6k+2 ; 6k+3
tick nha nguyễn thị mi
nguyễn thị mi
\(p=2\Rightarrow2^p+3^p=13\text{ ko là scp };\)
p> 2 => p lẻ 2^p chia 3 dư 2 => scp chia 3 dư 2 (vô lí)
=> k ton tai