cho a,bϵ Z : 4a2+3ab-11b2 ⋮5. CM: a4-b4 ⋮5
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

TG
10 tháng 4 2021
\(a^4+b^4-a^3b-ab^3=a^3\left(a-b\right)-b^3\left(a-b\right)=\left(a-b\right)\left(a^3-b^3\right)=\left(a-b\right)\left(a-b\right)\left(a^2+ab+b^2\right)=\left(a-b\right)^2\left(a^2+ab+b^2\right)\)
Có: \(\left\{{}\begin{matrix}\left(a-b\right)^2\ge0\\a^2+ab+b^2>0\end{matrix}\right.\)
\(\Rightarrow a^4+b^4-a^3b-ab^3\ge0\)
\(\Rightarrow a^4+b^4\ge a^3b+ab^3\)
10 tháng 4 2021
Áp dụng BĐT cosi với 2 số không âm:
`a^4+b^4+b^4+b^4>=4\root4{a^4b^12}=4|ab^3|>=4ab^3`
Hoàn toàn tương tự:
`b^4+a^4+a^4+a^4>=4a^3b`
`=>a^4+b^4+b^4+b^4+b^4+a^4+a^4+a^4>=4ab^3+4a^3b`
`<=>4(a^4+b^4)>=4(ab^3+a^3b)`
`<=>a^4+b^4>=ab^3+a^3b`

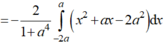
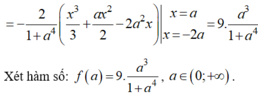
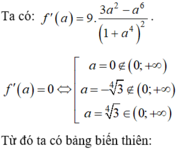
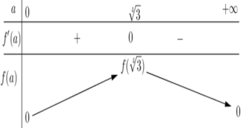

Ta có: \(4a^2+3ab-11b^2⋮5\)
\(\Leftrightarrow\left(5a^2+5ab-10b^2\right)-\left(4a^2+3ab-11b^2\right)⋮5\)
\(\Leftrightarrow5a^2+5ab-10b^2-4a^2-3ab+11b^2⋮5\)
\(\Leftrightarrow a^2+2ab+b^2⋮5\)
\(\Leftrightarrow\left(a+b\right)^2⋮5\)
\(\Leftrightarrow a+b⋮5\)(Vì 5 là số nguyên tố)
Ta có: \(a^4-b^4\)
\(=\left(a^2-b^2\right)\left(a^2+b^2\right)\)
\(=\left(a+b\right)\left(a-b\right)\left(a^2+b^2\right)⋮5\)(đpcm)