Giải tam giác DEF vuông tại E biết DE= 21cm EF=18cm
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{DF}{EF}=\dfrac{4}{5}\)
\(\Leftrightarrow DF=\dfrac{4}{5}EF\)
\(\Leftrightarrow DF=24\left(cm\right)\)
\(\Leftrightarrow FE=30\left(cm\right)\)
\(\Leftrightarrow DI=14.4\left(cm\right)\)

1.
Ta có:
\(\widehat{A}+\widehat{B}+\widehat{C}=180^0\)
Mà \(\widehat{B}=\widehat{C}\)
\(\Rightarrow\widehat{A}+\widehat{C}+\widehat{C}=180^0\)
\(\widehat{A}=180^0-2.65^0\)
\(\widehat{A}=50^0\)
2.
Áp dụng định lý pitago, ta có:
\(DF^2=DE^2+EF^2\)
\(\Rightarrow EF=\sqrt{DF^2-DE^2}=\sqrt{17^2-8^2}=\sqrt{225}=15cm\)
Ta có:
\(DF>EF>DE\)
\(\Rightarrow\widehat{E}>\widehat{D}>\widehat{F}\)

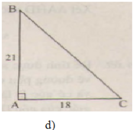
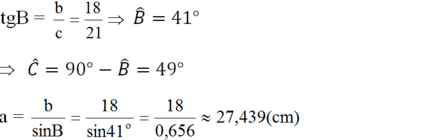
(Ghi chú: Bạn nên sử dụng các kí hiệu cạnh là a, b, c (thay vì BC, AC, AB) để đồng bộ với đề bài đã cho.
Cách để nhớ các cạnh là: cạnh nào thiếu chữ cái nào thì chữ cái đó là kí hiệu của cạnh đó. Ví dụ: cạnh AB thiếu chữ cái C nên c là kí hiệu của cạnh.
hoặc cạnh đối diện với góc nào thì đó chính là kí hiệu của cạnh. Ví dụ: cạnh đối diện với góc B là cạnh b (chính là cạnh AC))

a: Xét ΔEHD và ΔEHF có
EH chung
\(\widehat{HED}=\widehat{HEF}\)
ED=EF
Do đó: ΔEHD=ΔEHF
c: Ta có; ΔEHD=ΔEHF
=>HF=HD
mà H nằm giữa D và F
nên H là trung điểm của DF
=>\(HD=\dfrac{DF}{2}=3\left(cm\right)\)
ΔEHD vuông tại H
=>\(EH^2+HD^2=ED^2\)
=>\(EH^2=5^2-3^2=16\)
=>\(EH=\sqrt{16}=4\left(cm\right)\)
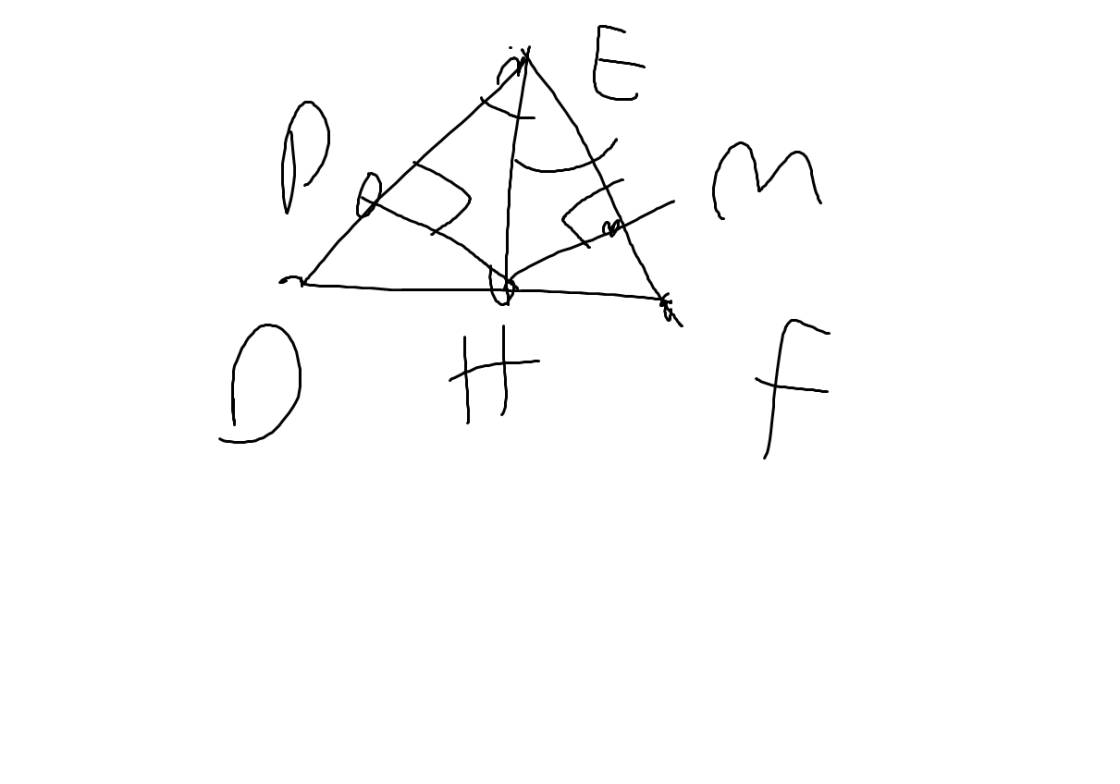
Áp dụng định lí Pytago vào ΔDEF vuông tại E, ta có
\(DF^2=DE^2+EF^2\)
\(\Leftrightarrow DF^2=21^2+18^2=765\)
\(\Leftrightarrow DF=\sqrt{765}=3\sqrt{85}cm\)
Xét ΔDEF vuông tại E có
\(\sin\widehat{D}=\frac{EF}{DF}=\frac{18}{3\sqrt{85}}=\frac{6}{\sqrt{85}}\)
\(\Rightarrow\widehat{D}\simeq40^036'\)
Ta có: ΔDEF vuông tại E(gt)
\(\Rightarrow\widehat{D}+\widehat{F}=90^0\)(hai góc nhọn phụ nhau)
\(\Rightarrow\widehat{F}=90^0-\widehat{D}=90^0-40^036'=49^024'\)
Vậy: \(DF=3\sqrt{85}cm\); \(\widehat{D}\simeq40^036'\); \(\widehat{F}=49^024'\)