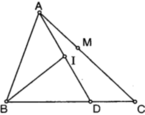
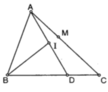
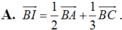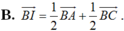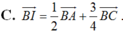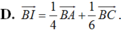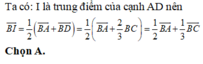Cho tam giác ABC. Gọi D là điểm định bởi vectơ BD=2/3 vectơ BC, I là trung điểm của AD. Gọi M là điểm thõa vectơ AM=x vectơ AC (x thuộc R)
a) Tính vectơ BI theo vectơ BA và vectơ BC.
b) Tính vectơ BM theo vectơ BA và vectơ BC.
c) Tính x để 3 điểm B, I, M thẳng hàng