trong 1 hộp có 100 viên bi đánh số từ 1 đến 100. có bnhieu cách chọn ra 3 viên bi sao cho tổng 3 số chia hết cho 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
16 tháng 6 2018
Không gian mẫu là số cách chọn ngẫu nhiên 3 viên bi từ hộp chứa 50 viên bi.
Suy ra số phần tử của không gian mẫu là 
.
Gọi A là biến cố “3 viên bi được chọn là một số chia hết cho 3 ’’.
Trong 50 viên bi được chia thành ba loại gồm: 16 viên bi có số chia hết cho 3; 17 viên bi có số chia cho 3 dư 1 và 17 viên bi còn lại có số chia cho 3 dư 2.
Để tìm số kết quả thuận lợi cho biến cố A, ta xét các trường hợp
● Trường hợp 1. 3 viên bi được chọn cùng một loại, có 
cách.
● Trường hợp 2. 3 viên bi được chọn có mỗi viên mỗi loại, có 
cách.
Suy ra số phần tử của biến cố A là 
.
Vậy xác suất cần tính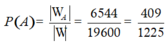 
Chọn B.
NV
Nguyễn Việt Lâm
Giáo viên
23 tháng 10 2020
Chia các số gồm 2 nhóm:
\(A=\left\{1;3;5;...;99\right\}\) gồm 50 số lẻ
\(B=\left\{2;4;6;...;100\right\}\) gồm 50 số chẵn
Chọn 3 viên thỏa mãn có tổng là chẵn khi: (3 viên cùng ở nhóm B); (2 viên nhóm A và 1 viên nhóm B)
Vậy số cách thỏa mãn là:
\(C_{50}^3+C_{50}^2.C_{50}^1=...\)
HP
5 tháng 11 2021
Có \(C_{24}^3\) cách chọn 3 viên bất kì.
Có \(C_8^3+C_6^3+C_{10}^3\) cách họn 3 viên bi cùng màu.
Có 6 cách chọn 3 viên bi cùng số.
\(\Rightarrow\) Có \(C_{24}^3-\left(C_8^3+C_6^3+C_{10}^3\right)-6=1822\) cách chọn 3 viên bi khác màu, khác số.
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 11 2021
Chọn 1 viên xanh: có 6 cách
Chọn 1 viên đỏ khác số viên xanh: 7 cách
Chọn 1 viên vàng khác số viên xanh và đỏ: 8 cách
Tổng cộng: \(6.7.8=336\) cách
CM
26 tháng 6 2017
Chọn A
Gọi x là số lần viên bi đỏ được chọn.
Gọi y là số lần viên bi xanh được chọn.
TH1. 1 ≤ x ≤ 6.
Có 6 cách chọn viên đỏ.
Có 5 cách chọn viên xanh.
=> Có 5.6 = 30 cách.
TH2. x = 7.
Có 6 cách chọn viên xanh.
=> Có 6 cách.
Vậy có 36 cách chọn.
CM
12 tháng 12 2019
Phương pháp:
Sử dụng quy tắc cộng và quy tắc nhân để làm bài toán.
Cách giải:
Vì số viên bi xanh ít hơn số viên bi đỏ nên ta lấy số viên bi xanh trước, số cách lấy 1 viên bi xanh có 6 cách .
Số cách lấy 1 viên bi đỏ và số của viên bi đỏ phải khác số của viên bi xanh đã lấy có 6 cách.
Như vậy có: 6 x 6 = 36 cách.
Chọn: A
CM
20 tháng 1 2019
Chọn C
20 viên bi khác nhau được đánh số từ 1 đến 20, chia làm ba phần:
Phần 1 gồm các viên bi mang số chia hết cho 3, có 6viên.
Phần 2 gồm các viên bi mang số chia cho 3 dư 1, có 7 viên.
Phần 3 gồm các viên bi mang số chia cho 3 dư 2, có 7 viên.
Lấy ba viên bi từ hộp trên rồi cộng số ghi trên đó lại, được một số chia hết cho 3 có các trường hợp sau:
Trường hợp 1: lấy được 3 viên bi ở phần 1, có C 6 3 cách.
Trường hợp 2: lấy được 3 viên bi ở phần 2, có C 7 3 cách.
Trường hợp 3: lấy được 3 viên bi ở phần 3, có C 7 3 cách.
Trường hợp 4: lấy được 1 viên bi ở phần 1, 1 viên bi ở phần 2 và 1 viên bi ở phần 3, có C 6 1 . C 7 1 . C 7 1 cách.
Vậy có 
cách lấy được ba viên bi thỏa mãn yêu cầu bài toán.
Chia các số từ 1 đến 100 thành 3 nhóm:
\(A=\left\{1;4;7;...;100\right\}\) gồm 34 số chia 3 dư 1
\(B=\left\{3;6;9;...;99\right\}\) gồm 33 số chia hết cho 3
\(C=\left\{2;5;...;98\right\}\) gồm 33 số chia 3 dư 2
3 viên bi có tổng chia hết cho 3 khi chúng thỏa mãn: 3 viên cùng 1 nhóm hoặc 3 viên nằm ở 3 nhóm khác nhau
Vậy có: \(C_{34}^3+C_{33}^3+C_{33}^3+C_{34}^1.C_{33}^1.C_{33}^1=...\) số cách thỏa mãn