Cho x,y là các số thực thỏa mãn 4x^2 + y^2= 8+3xy
Tìm GTLN của biểu thức P = xy +2020
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: \(4x^2+y^2=8+3xy\Leftrightarrow4x^2-4xy+y^2=8-xy\)
\(\Leftrightarrow\left(2x-y\right)^2=8-xy\ge0\forall x,y\inℝ\Rightarrow xy\le8\)
\(\Rightarrow P=xy+2020\le8+2020=2028\)
Đẳng thức xảy ra khi \(\hept{\begin{cases}2x=y\\xy=8\end{cases}}\Rightarrow\left(x,y\right)\in\left\{\left(2;4\right);\left(-2;-4\right)\right\}\)

Ta co : \(x^2+y^2-4x+3=0\)
\(=>\left(x-2\right)^2+y^2=1\)
\(=>\left(x-2\right)^2\le1=>x\le3\)
Lai co : \(x^2+y^2=4x-3\le4.3-3=9\)
Dau = xay ra \(< =>\hept{\begin{cases}x=4\\y=0\end{cases}}\)
Vay gtln cua P = 9 khi x = 4 ; y = 0
(sai thi bo qua cho minh vi lan dau lam dang nay)

Đáp án B
Ta có:
3 x 2 + y 2 − 2 . log 2 x − y = 1 2 1 + log 2 1 − x y ⇔ 3 x 2 + y 2 − 2 . log 2 x − y 2 = log 2 2 − 2 x y
⇔ 3 x 2 + 2 x y + y 2 − 2 + 2 x y . log 2 x − y 2 = log 2 2 − 2 x y ⇔ 3 x − y 2 . log 2 x − y = 3 2 − 2 x y . log 2 2 − 2 x y
Xét hàm số f t = 3 t . log 2 t trên khoảng 0 ; + ∞ , có f ' t = 3 t ln 3. log 2 t + 3 t t . ln 2 > 0 ; ∀ t > 0
Suy ra f t là hàm số đồng biến trên 0 ; + ∞ mà
f x − y 2 = f 2 − 2 x y ⇒ x 2 + y 2 = 2
Khi đó:
M = 2 x 3 + y 3 − 3 x y = 2 x + y x + y 2 − 3 x y − 3 x y ⇔ 2 M = 2 x + y 2 x + y 2 − 3.2 x y − 3.2 x y 2 x + y 2 x + y 2 − 3 x + y 2 + 6 − 3 x + y 2 + 6 = 2 x + y 6 − x + y 2 − 3 x + y 2 + 6 = − 2 a 3 − 3 a 2 + 12 a + 6 ,
Với a = x + y ∈ 0 ; 4
Xét hàm số f a = − 2 a 3 − 3 a 2 + 12 a + 6 trên 0 ; 4 ,
suy ra m ax 0 ; 4 f a = 13.
Vậy giá trị lớn nhất của biểu thức M là 13 2

Đáp án B
Ta có
3 x 2 + y 2 − 2 . log 2 x − y = 1 2 1 + log 2 1 − x y ⇔ 3 x 2 + y 2 − 2 . log 2 x − y 2 = log 2 2 − 2 x y
⇔ 3 x 2 + 2 x y + y 2 − 2 + 2 x y . log 2 x − y 2 = log 2 2 − 2 x y ⇔ 3 x − y 2 . log 2 x − y = 3 2 − 2 x y . log 2 2 − 2 x y
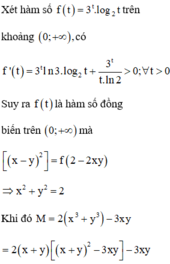
⇔ 2 M = 2 x + y 2 x + y 2 − 3.2. x y − 3.2 x y = 2 x + y 2 x + y 2 − 3 x + y 2 + 6 − 3 x + y 2 + 6
= 2 x + y 6 − x + y 2 − 3 x + y 2 + 6 = − 2 a 3 − 3 a 2 + 12 a + 6 ,
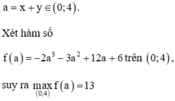
Vậy giá trị lớn nhất của biểu thức M là 13 2

\(1=x+y+3xy\le x+y+\dfrac{3}{4}\left(x+y\right)^2\)
\(\Rightarrow3\left(x+y\right)^2+4\left(x+y\right)-4\ge0\)
\(\Rightarrow3\left(x+y+2\right)\left(x+y-\dfrac{2}{3}\right)\ge0\)
\(\Rightarrow x+y\ge\dfrac{2}{3}\) \(\Rightarrow\dfrac{1}{x+y}\le\dfrac{3}{2}\)
Đồng thời: \(x^2+y^2\ge\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{1}{2}.\left(\dfrac{2}{3}\right)^2=\dfrac{2}{9}\)
\(\Rightarrow-\left(x^2+y^2\right)\le-\dfrac{2}{9}\)
Từ đó ta có:
\(A=\sqrt{1-x^2}+\sqrt{1-y^2}+\dfrac{1-\left(x+y\right)}{x+y}=\sqrt{1-x^2}+\sqrt{1-y^2}+\dfrac{1}{x+y}-1\)
\(A\le\sqrt{2\left[2-\left(x^2+y^2\right)\right]}+\dfrac{1}{x+y}-1\le\sqrt{2\left(2-\dfrac{2}{9}\right)}+\dfrac{3}{2}-1=\dfrac{3+8\sqrt{2}}{6}\)
Dấu "=" xảy ra khi \(x=y=\dfrac{1}{3}\)
\(3xy+8=4x^2+y^2\ge4xy\)
\(\Rightarrow xy\le8\)
\(\Rightarrow P\le8+2020=2028\)
\(P_{max}=2028\) khi \(2x=y=\pm4\)