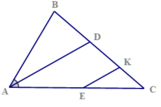
Δ ABC có A = 60 , có AD là phân giác của AE ∈ AC . Qua E vẽ đường thằng // với AD cắt BC ở K
a) tính CAD
b) tính CEK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 3 2019
a) C A D ^ = C A B ^ 2 = 60 0 2 = 30 0 (AD là tia phân giác)
b) C E K ^ = C A D ^ = 30 0 (cặp góc đồng vị; EK // AD)
9 tháng 8 2016
a. xét tam giác CEF và tam giác FBD có
DF là cạnh chung
góc EDF=góc DFB ( so le trong của DE//BC)
góc BDF = góc EDF ( so le trong của EF//AB)
=> tam giác CEF= tam giác EBD(G.C.G)
=> EF=DB ( 2 cạnh tương ứng )
mà BD=AD(D là trung điểm của AB)
=>EF=AD ( đpcm)
b. ta có :
BDF+FDE+EDA=1800
BFD+DFE+EFC=1800
MÀ BDF=EFD ( theo a)
FDE=DBF ( theo a)
=> góc EDA= góc EFC
Xét tam giác ADF và EFC có :
EF=AD ( cmt )
EDA=EFC (cmt)
FEC=EAD ( đồn vị của EF//AB)
=> tam giác ADE = tam giác EFC (G.C.G)
c, vì theo a ta có
tam giác ADE= tam giác EFC (G.C.G)
=> AE=EC ( 2 cạnh tương ứng )
7 tháng 8 2017
a/ ta có A=60 mà AD là tia phân giác
=> CAD= 1/2 A = 1/2.60= 30
b/ ta có CEK=CAD ( 2 góc đồng vị, EK//AD)
=> CEK= 30
14 tháng 4 2023
2:
a: Xét ΔBAD vuông tại A và ΔBED vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
=>BA=BE và DA=DE
=>BD là trung trực của AE
b: Xét ΔDAF vuông tại A và ΔDEC vuông tại E có
DA=DE
góc ADF=góc EDC
=>ΔDAF=ΔDEC
=>DF=DC
c: AD=DE
DE<DC
=>AD<DC
d: Xét ΔBFC co BA/AF=BE/EC
nên AE//CF